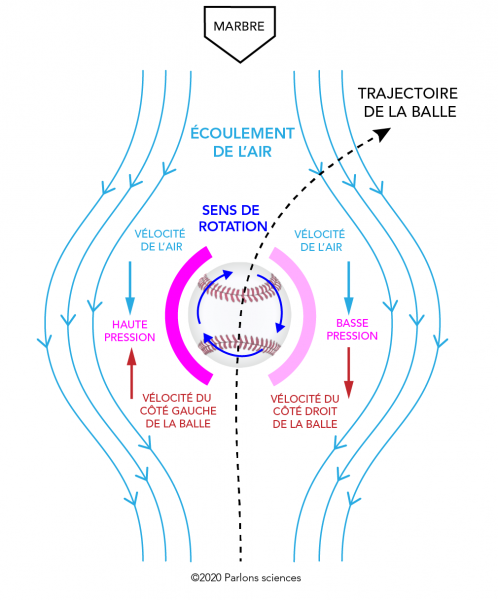
Pourquoi les balles courbe dévient-elles?

Lanceur tenant une balle de baseball (Pgiam, iStockphoto)

Lanceur tenant une balle de baseball (Pgiam, iStockphoto)
7.87
Quels sont les liens avec mon programme d'études?
Curriculum Alignment
AB
10
Connaissances et employabilité Sciences 10-4 (2007)
Unité B : Comprendre les technologies de transfert d’énergie
BC
11
Physique 11 (Août 2018)
Grandes idée: Le mouvement d’un objet peut être prédit, analysé et décrit.
BC
12
Physique 12 (Août 2018)
Grandes idée: Les mesures des grandeurs d’un mouvement dépendent du système de référence, ou référentiel, dans lequel le mouvement est étudié.
NU
10
Connaissances et employabilité Sciences, 10-4, 20-4 (Alberta, 2007)
Unité B : Comprendre les technologies de transfert d’énergie
NU
10
Sciences 10 (Alberta, 2005, Révision 2014)
Unité B: Flux d’énergie dans les systèmes technologiques
NU
10
Sciences 14-24 (Alberta, 2004, Révision 2014)
Unité B: Comprendre les technologies de transfert d’énergie
NU
11
Sciences 24 (Alberta, 2004, Révision 2014)
Unité D: Mouvement, changement et sécurité des transports
YT
11
Physique 11 (Colombie britannique, Août 2018)
Grandes idée: Le mouvement d’un objet peut être prédit, analysé et décrit.
YT
12
Physique 12 (Colombie britannique, Août 2018)
Grandes idée: Les mesures des grandeurs d’un mouvement dépendent du système de référence, ou référentiel, dans lequel le mouvement est étudié.
NT
10
Connaissances et employabilité Sciences, 10-4, 20-4 (Alberta, 2007)
Unité B : Comprendre les technologies de transfert d’énergie
NT
10
Sciences 10 (Alberta, 2005, Révision 2014)
Unité B: Flux d’énergie dans les systèmes technologiques
NT
10
Sciences 14-24 (Alberta, 2004, Révision 2014)
Unité B: Comprendre les technologies de transfert d’énergie
NT
11
Sciences 24 (Alberta, 2004, Révision 2014)
Unité D: Mouvement, changement et sécurité des transports
AB
8
Connaissances et employabilité Sciences, 8e et 9e années (2007)
Unité A: Mélanges et circulation de la matière
AB
8
Sciences 7e, 8e et 9e années Programme d'études (Révision 2014)
Unité A: Mélanges et circulation de la matière
NS
8
Sciences 8e année (2020-21)
Les apprenants mettront à l'essai les effets des changements de température et de pression sur les propriétés des fluides.
NU
8
Connaissances et employabilité Sciences, 8e années (Alberta, 2007)
Unité A: Mélanges et circulation de la matière