Qu’est-ce qu’une fractale?

Delta de la rivière Saskatchewan, Manitoba (Elen11, iStockphoto)

Delta de la rivière Saskatchewan, Manitoba (Elen11, iStockphoto)
Quels sont les liens avec mon programme d'études?
Découvre ce que sont les fractales et essaie d’en fabriquer toi-même!

Image - Version texte
Voici un dessin informatique en couleur de la fougère de Barnsley. L'image est composée de folioles vertes qui se ramifient à partir d'une tige verte principale. Les folioles deviennent de plus en plus petites à mesure que l'on monte sur la tige. Les folioles sont des copies exactes de la fougère dans son ensemble, mais à une échelle plus petite. Elles deviennent également plus petites à mesure qu'elles s'éloignent de la tige.
Lorsque tu regardes la photo ci-dessus, que vois-tu? Vois-tu la feuille d’une fougère, ou vois-tu un motif complexe et répétitif de fougères qui semble s’étendre à l’infini?
L’image ci-dessus est connue sous le nom de fougère de Barnsley. La fougère de Barnsley n’est pas une vraie fougère, mais plutôt un exemple de fractale.
Le savais-tu?
La fougère de Barnsley doit son nom au mathématicien britannique Michael Barnsley qui l’a décrite pour la première fois dans son livre Fractals Everywhere.
Les fractales sont des figures géométriques, tout comme les rectangles, les cercles et les carrés. Mais contrairement à ces figures géométriques, les fractales ont des propriétés particulières.
Les propriétés des fractales
Les fractales sont typiquement autosimilaires
Les objets géométriques, telles que les figures à deux dimensions, sont similaires s’ils ont la même forme.
Par exemple, les deux carrés de gauche sont similaires parce qu’ils ont la même forme, même s’ils sont de tailles différentes. Les deux rectangles de droite ne sont PAS similaires, car ils n’ont pas la même forme.
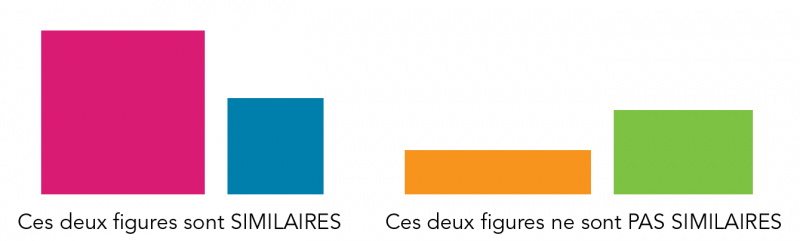
Image - Version Texte
Dans la partie gauche de l’image se trouvent deux carrés. Il y a un grand carré magenta et un petit carré bleu. Ces deux figures sont considérées comme similaires l’une à l’autre, car elles ont la même forme. Dans la partie droite de l’image se trouvent deux rectangles. Il y a un long rectangle orange de petite largeur, et un rectangle vert, plus large. Ces deux figures ne sont pas similaires l’une à l’autre, car elles n’ont pas la même forme.
Les figures à deux dimensions qui sont autosimilaires sont constituées de formes qui sont des copies plus petites de la forme originale. Par exemple :
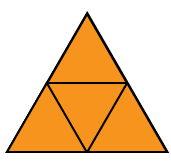
Image - Version Texte
Illustration d’un triangle équilatéral orange. Le triangle est divisé en quatre triangles équilatéraux plus petits et similaires.

Image - Version Texte
Illustration d’un carré vert. Le carré est divisé en quatre carrés plus petits et similaires.
Question 1: Les hexagones sont-ils autosimilaires? Peux-tu former de grands hexagones à partir de plus petits? Fais un essai en utilisant des blocs géométriques. Voir la réponse en bas de la page.
Les fractales ont des composantes répétitives
L’un des aspects intéressants à propos des fractales est que ces formes autosimilaires peuvent être utilisées pour composer des motifs (ou régularités) qui peuvent se répéter indéfiniment! Il s’agit de l’autre élément clé de ce qu’être une fractale signifie.

Image - Version Text
Trois motifs de damiers noirs et blancs sont représentés. L’image de gauche est un damier de 2 par 2, l’image du centre est un damier de 4 par 4 et l’image de droite est un damier de 8 par 8. Au cas où tu l’ignorerais, un damier est un motif de grille alternant le noir et le blanc.
Exemples de fractales
Le triangle de Sierpinski
Un exemple célèbre de fractale qui repose sur la forme autosimilaire d’un triangle est le triangle de Sierpinski. Cette fractale porte le nom du mathématicien polonais Wacław Sierpiński qui l’a décrite en 1915.
Voici comment procéder pour créer cette fractale :

Image - Version Texte
Dessin au trait noir d’un triangle équilatéral blanc.
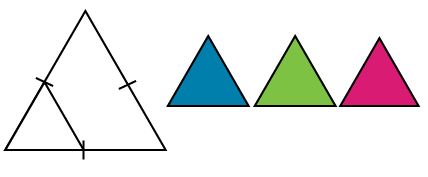
Image - Version Texte
Quatre triangles sont représentés. Le triangle à l’extrême gauche est un dessin au trait noir. Les repères placés sur chacun des côtés indiquent le point central de chaque ligne. Une ligne reliant deux des repères délimite un nouveau triangle réduit de moitié à l’intérieur du grand triangle. À côté du triangle blanc se trouvent trois triangles aux dimensions réduites de moitié par rapport au grand triangle blanc. L’un est bleu, l’autre est vert et le troisième est magenta.
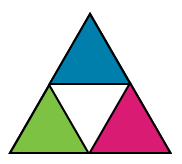
Image - Version Texte
L’illustration montre le contour d’un grand triangle équilatéral. À l’intérieur de celui-ci se trouvent quatre triangles équilatéraux plus petits dont les coins se touchent. Trois des triangles s’insèrent dans chaque coin du grand triangle et un quatrième s’insère entre eux au centre. Le petit triangle du haut est bleu, le triangle du centre est blanc, le triangle en bas à gauche est vert et le triangle en bas à droite est magenta.
Le savais-tu?
Une autre façon de créer cette forme est de découper un trou en forme de triangle au centre de chaque triangle.
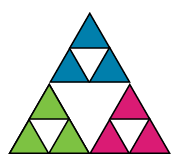
Image - Version Texte
L’illustration montre trois ensembles de triangles similaires à ceux de l’étape 3. Ils sont reliés de manière à former une pyramide. L’ensemble des trois triangles du haut est bleu, l’ensemble des triangles en bas à gauche est vert et l’ensemble des triangles en bas à droite est magenta. Comme à l’étape 3, des triangles blancs sont centrés dans chaque groupe de triangles colorés.
Question 2: Dessine et colorie les deux prochains triangles de Sierpinski de cette série. Tu auras besoin d’un crayon bien taillé et d’une règle. Voir la réponse en bas de la page.
Tu peux également créer des fractales à partir de formes similaires, mais non autosimilaires. Par exemple, un cercle n’est pas autosimilaire, car il ne peut pas être composé de cercles plus petits. Cependant, tu peux créer des fractales intéressantes en utilisant des cercles.
La baderne d’Apollonius
Une célèbre fractale utilisant des cercles porte le nom de baderne d’Apollonius (ou cercles d’Apollonius). Elle doit son nom au mathématicien grec Apollonius de Perga (vers 262-190 avant notre ère).
Voici comment procéder pour créer cette fractale :
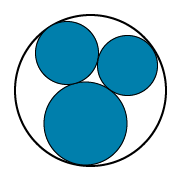
Image - Version Texte
L’illustration montre le dessin au trait noir d’un grand cercle. À l’intérieur de ce cercle se trouvent trois autres cercles plus petits qui se touchent et qui touchent le grand cercle. Les petits cercles sont colorés en bleu.
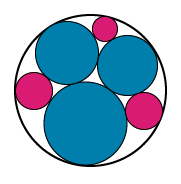
Image - Version Texte
Dans l’image représentée à l’étape 1, trois autres cercles ont été ajoutés. Ces cercles encore plus petits sont situés dans les espaces blancs entre les trois cercles initiaux et le cercle extérieur. Les trois cercles additionnels sont colorés en magenta.
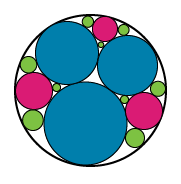
Image - Version Texte
Dans l’image représentée à l’étape 2, neuf autres cercles ont été ajoutés. Ces cercles, encore plus petits, sont situés dans les espaces blancs entre les six cercles initiaux et le cercle extérieur. Les neuf cercles additionnels sont colorés en vert.
Ce qui fait qu’il s’agit d’une fractale, c’est que tu peux continuer à ajouter des cercles de plus en plus petits dans les espaces un nombre infini de fois.
Définition d’infini :: quelque chose qui ne s’arrête jamais.
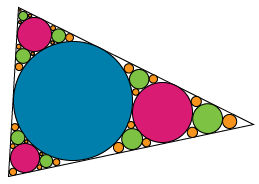
Image - Version Text
L’illustration montre le dessin au trait noir d’un triangle rempli de la même façon que dans les exemples montrés plus haut. Le plus grand cercle du triangle est en bleu. Les petits cercles suivants sont en magenta, les plus petits cercles suivants sont en vert et les cercles encore plus petits sont en orange.
Choisis une forme et crée ta propre œuvre d’art inspirée de la baderne d’Apollonius!
Le flocon de Koch
Il est également possible de créer une fractale en modifiant la forme elle-même. Le flocon de Koch (ou courbe de Koch) en est un exemple bien connu. Cette fractale a été décrite pour la première fois par le mathématicien suédois Helge von Koch en 1904.
Voici comment procéder pour créer cette forme :

Image - Version Texte
L’illustration montre le dessin au trait d’un triangle équilatéral. La ligne est colorée en orange.
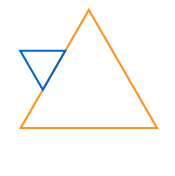

Image - Version Texte
Deux images sont présentées. Dans l’image du haut, on voit le dessin au trait orange d’un triangle équilatéral. Un autre triangle équilatéral, d’un tiers de la dimension du triangle orange, est relié côté à côté au milieu du côté gauche du triangle orange. La couleur de ce petit triangle contigu (qui touche, qui est voisin) est bleue.
Dans l’image du bas, le segment où les deux côtés du triangle sont reliés a été supprimé. On dirait maintenant qu’il y a une pointe bleue qui sort sur le côté du triangle orange.

Image - Version Texte
L’image représente une étoile à six branches. Les lignes de trois des pointes sont en orange et les lignes des trois autres pointes sont en bleu. Les pointes orange alternent avec les pointes bleues.
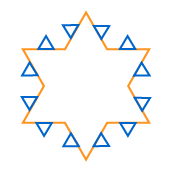

Image - Version Texte
Deux images sont présentées. L’image du haut est un dessin au trait d’une étoile orange à six branches. Sur chaque pointe ont été ajoutés deux dessins au trait bleus plus petits représentant des triangles. Chacun des petits triangles fait un tiers de la dimension de la pointe de l’étoile.
L’image du bas représente la même forme, mais cette fois, le segment où les côtés des triangles sont reliés à l’étoile a été supprimé. La forme ressemble maintenant à un flocon de neige orange.

Image - Version Texte
L’illustration montre un dessin au trait orange d’une forme qui ressemble à un flocon de neige complexe. Cette forme a 66 pointes.
En répétant ce motif de très nombreuses fois, tu obtiens une fractale! Tu trouveras ci-dessous une animation des sept premières étapes, ou itérations, de la forme.
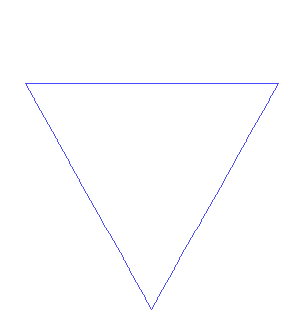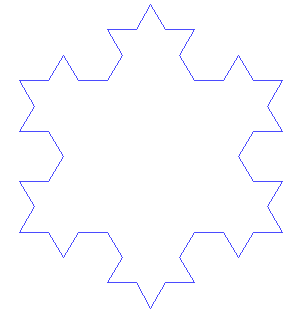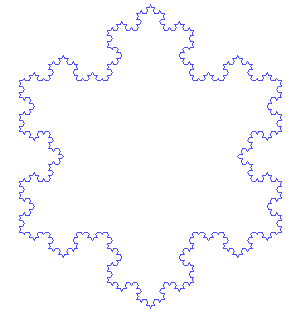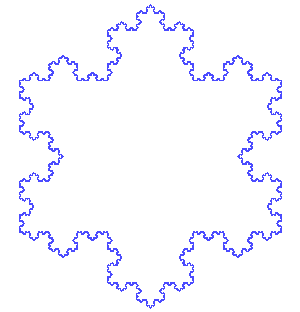
Animation des sept premières itérations du flocon de Koch. (Source : Image du domaine public par António Miguel de Campos via Wikimedia Commons.)
Image - Version Texte
Animation des sept premières itérations du flocon de Koch.
L’ensemble de Mandelbrot
Les trois fractales que nous avons examinées jusqu’à présent sont toutes créées à l’aide d’un processus appelé itération. Pour faire simple, cela signifie que tu pars d’une forme et d’un motif spécifiques, que tu ajustes et que tu répètes encore et encore.
Mais ce n’est pas la seule façon de créer des fractales. L’une des fractales les plus célèbres est l’ensemble de Mandelbrot. Elle doit son nom au mathématicien Benoît Mandelbrot (1924-2010), qui l’a étudiée et rendue populaire. Il l’a découverte lorsqu’il a remarqué une régularité répétitive (ou motif répétitif) autosimilaire dans un autre ensemble qu’il enseignait, l’ensemble de Julia. Il n’a pu faire cette découverte que parce qu’il a eu accès à des ordinateurs IBM tout neufs.

Comme pour le flocon de Koch, lorsque tu zoomes sur les formes rondes le long des bords de l’ensemble de Mandelbrot, tu peux observer qu’elles sont autosimilaires!

En zoomant sur la forme de gauche de l’ensemble de Mandelbrot, tu peux observer l’autosimilarité. (Source : Image du domaine public via Wikimedia Commons.)
Attention aux idées fausses
Les images comme celles ci-dessus n’ont PAS été dessinées à la main! Elles ont été réalisées sur ordinateur à l’aide d’équations mathématiques complexes pour déterminer les points où les formes peuvent apparaître.
OPTIONNEL : Découvres-en davantage sur les mathématiques de l’ensemble de Mandelbrot.
La particularité de la fractale de l’ensemble de Mandelbrot est qu’il s’agit d’un ensemble de nombres. Par exemple, tous les nombres naturels de 1 à 5 peuvent être considérés comme un ensemble. Nous pouvons le décrire en utilisant la notation d'ensemble (ou notation ensembliste). Cela ressemblerait à ceci :
{1, 2, 3, 4, 5}
Les éléments d’un ensemble sont séparés par des virgules et placés entre crochets.
Nous pouvons également décrire cet ensemble en mots, ou en notation sémantique. Dans le cas ci-dessus, nous pourrions dire : « L’ensemble A est un ensemble composé des cinq premiers nombres naturels. »
Les ensembles peuvent contenir à la fois des listes finies et infinies de nombres.
L’ensemble A = {1, 2, 3, 4, 5} (les cinq premiers nombres naturels) est un ensemble fini parce qu’il n’y a que certains nombres qui répondent à la règle « les cinq premiers nombres naturels ».
Nous pouvons également avoir des ensembles infinis de nombres. Par exemple, si notre ensemble était « tous les multiples de 3 », il pourrait inclure une liste infinie de nombres. Nous pourrions le présenter en notation ensembliste et en notation sémantique comme suit :
{3, 6, 9, 12, …} (tous les multiples de 3)
Des règles ou des fonctions très complexes peuvent être appliquées aux ensembles pour générer les nombres qui les composent.
Supposons que l’on veuille créer un ensemble qui soit une suite dans laquelle chaque nombre de l’ensemble est un entier naturel plus grand que le précédent. Pour ce faire, nous pourrions utiliser une suite récursive. Cela signifie essentiellement que tu prends un nombre et que tu lui appliques une fonction pour obtenir le nombre suivant dans la suite. Nous utilisons une notation un peu spéciale pour illustrer cela.
Nous utilisons une variable appelée X et nous utilisons un petit nombre sous le X (un indice) pour indiquer où se trouve le nombre dans la suite.
L’exemple précédent :
{1, 2, 3, 4, 5}
pourrait être réécrit comme suit :
{X1, X2, X3, X4, X5}
Un nombre en nième position dans la suite est Xn.
Alors, comment pourrions-nous utiliser cette notation pour expliquer comment créer la suite de 1 à 5 ? Ce cas est simple, car la position dans la suite et le nombre sont les mêmes.
Xn = n
Pour le premier nombre dans la suite, X1 = 1. Est-ce que ça correspond? Oui! Essaie toi-même pour X2, X3, X4 et X5.
Créer une régularité (ou un motif) est assez facile lorsque la formule est simple comme celle-ci. Mais la formule peut être beaucoup plus complexe.
Question 3: Trouve les cinq premiers nombres d’une suite dont la régularité est Xn = n2 + 1. Voir la réponse en bas de la page.
L’ensemble de Mandelbrot utilise des règles assez complexes tant pour la fonction que pour l’endroit où les nombres peuvent et ne peuvent pas commencer. Il utilise même des nombres réels et imaginaires! Si tu souhaites en apprendre davantage, consulte les liens proposés dans la section « Pour en savoir plus » ci-dessous.
Les fractales dans la vie de tous les jours
Les fractales dans la nature
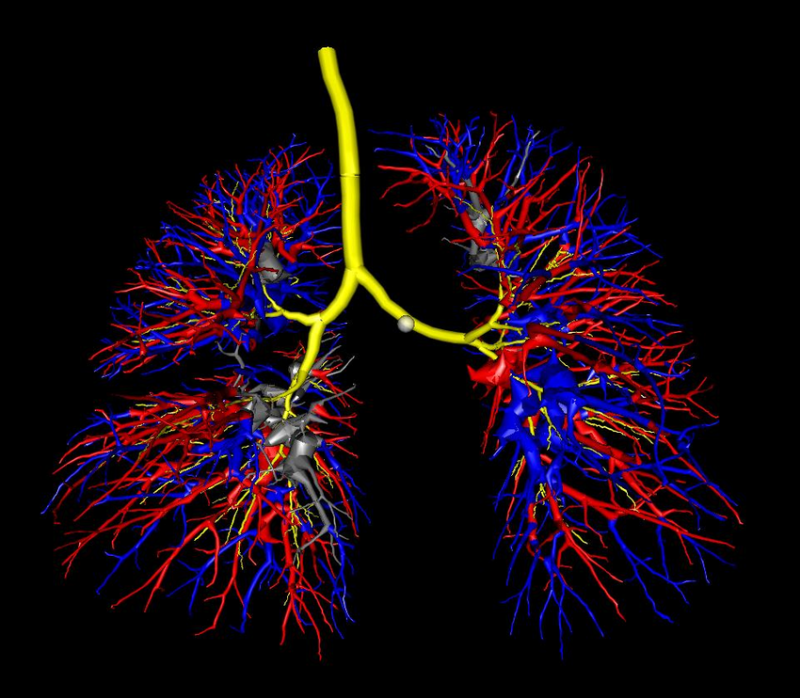
Image - Version Texte
Cette image est une image de synthèse des artères, des veines et des voies respiratoires des poumons. Les voies respiratoires sont colorées en jaune. La voie aérienne principale est une ligne épaisse qui descend verticalement. Elle se divise ensuite en deux pour chacun des deux poumons. Il y a d'autres ramifications une fois que les voies respiratoires sont dans les poumons. Les artères sont colorées en rouge. Elles forment un réseau dense de ramifications autour des voies respiratoires de chaque poumon. Les veines sont bleues et présentent un schéma de ramification similaire à celui des artères.

Image - Version Texte
Photographie en couleur d'une tête de chou Romanesco, ou fractal. La couleur générale du chou est un vert jaunâtre pâle. La partie que nous mangeons, qui est constituée de boutons de fleurs, forme un motif en spirale. Chaque bourgeon est composé d'une série de bourgeons plus petits, tous disposés selon un autre motif en spirale. Ce sont ces motifs autosimilaires qui le font ressembler à une fractale.
Les fractales dans l’art
La deuxième réponse est liée à la « beauté » des fractales. Les gens semblent être fascinés par les fractales! Fais une recherche Web sur l’art fractal et explore certaines des étonnantes galeries d’images que les gens ont créées avec différentes fractales.
Ou encore, fais une recherche sur le Web pour trouver de la musique fractale et tu découvriras de la musique créée par des personnes utilisant des fractales. Au lieu de créer des images, ils créent des motifs autosimilaires et répétitifs avec des notes de musique. Tout comme lorsqu’on regarde des images fractales, lorsqu’on écoute de la musique fractale, il est souvent facile d’oublier qu’elle a été créée à partir d’un ensemble d’équations mathématiques!
Quelqu’un d’autre a même transformé des parties de l’ensemble de Mandelbrot, ainsi que d’autres fractales intéressantes, en sons!
Des applications pratiques des fractales
Les fractales ont également été utilisées à de nombreuses fins pratiques. En géologie, la géométrie fractale est utilisée pour comprendre comment le pétrole s’écoule dans les réservoirs souterrains et pour localiser les gisements de pétrole. Les fractales permettent également de créer des modèles du fonctionnement des tremblements de terre.
En ingénierie, la géométrie fractale a été utilisée pour tester les contraintes sur les plateformes pétrolières et les avions. En médecine, la géométrie fractale a été utilisée pour étudier les profils de la marche de patients atteints de la maladie de Parkinson afin de comprendre la gravité de leurs symptômes.
L’armée utilise les fractales pour distinguer les éléments naturels des éléments artificiels sur les cartes aériennes, et les fractales ont été utilisées dans la conception d’un meilleur camouflage pour les uniformes militaires. Les scientifiques ont également utilisé les fractales pour rechercher des objets artificiels sur les surfaces planétaires.
Les fractales et le changement climatique
Les fractales sont également utilisées pour nous aider à mieux comprendre la Terre et les impacts du changement climatique. La compréhension des formes et des tailles d’éléments tels que les nuages, les forêts, les bassins et les rivages peut aider les scientifiques à modéliser plus précisément les systèmes climatiques et l’impact du changement climatique sur ces systèmes.
Par exemple, les fractales peuvent aider des équipes de recherche à comprendre les surfaces de formes très irrégulières, comme la forme d’une feuille ou le couvert forestier. Cela peut les aider à faire de meilleures estimations de choses comme la capture du carbone lors de la photosynthèse. Pour ce faire, elles utilisent ce que l’on appelle les dimensions fractales. Pour faire simple, cela signifie que plus l’échelle utilisée pour mesurer quelque chose est petite, plus la mesure est précise.
Par exemple, imaginons que nous voulions mesurer la superficie et le périmètre d’une île de forme irrégulière. Comment pourrait-on s’y prendre? L’une des façons serait de créer des carrés d’une certaine taille et de voir combien d’entre eux couvriraient la forme de l’île. Il est important de noter que nous ne comptons que les carrés qui couvrent uniquement la terre et non l’eau.
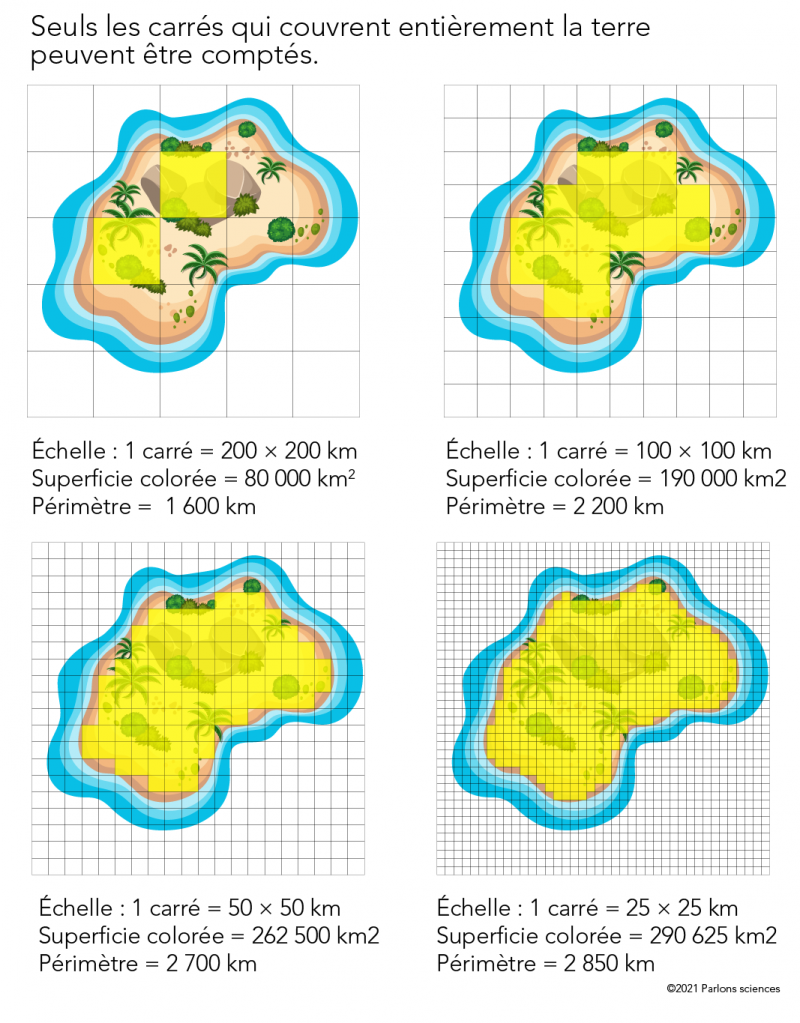
Image - Version Texte
Voici quatre images de la même illustration d’une île tropicale de forme irrégulière. Une grille est superposée à chacune d’elles.
Sur l’île en haut à gauche, une grille de 5 par 5 recouvre l’île. Toute partie de l’île qui occupe l’intégralité d’un ans l’un des carrés de la grille est colorée en jaune. Pour cette île, 2 carrés sont colorés. L’échelle de la grille est de 200 par 200 kilomètres. Par conséquent, cette île a une superficie colorée de 80 000 kilomètres carrés et un périmètre de 1 600 kilomètres.
Sur l’île en haut à droite, une grille de 10 par 10 recouvre l’île. Toute partie de l’île qui occupe l’intégralité d’un des carrés de la grille est colorée en jaune. Pour cette île, 19 carrés sont colorés. L’échelle de la grille est de 100 par 100 kilomètres. Par conséquent, cette île a une superficie colorée de 190 000 kilomètres carrés et un périmètre de 2 200 kilomètres.
Sur l’île en bas à gauche, une grille de 20 par 20 recouvre l’île. Toute partie de l’île qui occupe l’intégralité d’un des carrés de la grille est colorée en jaune. Pour cette île, 105 carrés sont colorés. L’échelle de la grille est de 50 par 50 kilomètres. Par conséquent, cette île a une superficie colorée de 262 500 kilomètres carrés et un périmètre de 2 700 kilomètres.
Sur l’île en bas à droite, une grille de 40 par 40 recouvre l’île. Toute partie de l’île qui occupe l’intégralité d’un des carrés de la grille est colorée en jaune. Pour cette île, 465 carrés sont colorés. L’échelle de la grille est de 25 par 25 kilomètres. Par conséquent, cette île a une superficie colorée de 290 625 kilomètres carrés et un périmètre de 2 850 kilomètres.
Lorsque les carrés sont grands, nous ne pouvons pas mettre beaucoup de carrés. Mais si nous utilisions des carrés plus petits, nous pourrions en mettre plus. Nous pourrions continuer en utilisant des carrés de plus en plus petits. Plus les carrés sont petits, plus nous nous rapprochons de la taille réelle de l’île. D’après toi, quelle serait la plus petite taille de carré que tu pourrais utiliser? Techniquement, il n’y en a pas. Tu pourrais continuer à créer des carrés de plus en plus petits à l’infini! C’est ce qui fait de ce type de mesure une fractale. Comme tu peux le voir dans l’image ci-dessus, plus nous réduisons la taille des carrés que nous utilisons pour mesurer, plus nous couvrons de surface sur l’île. Cela devrait te rappeler le flocon de Koch!
Les fractales sont partout, quand on sait où regarder!
RÉPONSES
Q1: Non, les hexagones ne sont pas autosimilaires de la même manière que les carrés et les triangles équilatéraux.

Image - Version Texte
Cinq images d’hexagones alignés sont représentées. Le premier hexagone a un contour noir et est coloré en bleu clair. Le deuxième hexagone contient sept hexagones plus petits, colorés en violet. Six petits hexagones s’insèrent dans chacun des sommets du grand hexagone et le septième se trouve au centre. Les parties du grand hexagone non couvertes par les petits hexagones sont colorées en bleu clair. Le troisième hexagone contient également sept petits hexagones. Ils sont colorés en rouge. Cette fois, les six petits hexagones ont chacun un côté qui touche le centre d’un côté extérieur du grand hexagone. Le septième hexagone s’insère parfaitement au centre des six autres petits hexagones. Les parties du grand hexagone non couvertes par les petits hexagones sont colorées en bleu clair. Le quatrième grand hexagone contient trois hexagones. Ils sont colorés en bleu foncé. Ils s’insèrent dans trois sommets alternés du grand hexagone. Les parties du grand hexagone non couvertes par les petits hexagones sont colorées en bleu clair. Le cinquième hexagone est divisé par des lignes noires qui s’étendent horizontalement et diagonalement, formant des rangées d’hexagones. Cet hexagone est également coloré en bleu clair.
Q2: Les deux prochains triangles de Sierpiński de cette série ressembleraient à ceci.
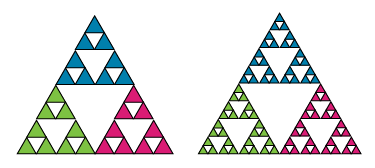
Image - Version Texte
Deux images sont présentées. L’image de gauche est un triangle de Sierpinski créé à partir de 27 petits triangles et l’image de droite est un triangle de Sierpinski créé à partir de 81 petits triangles. Dans chacun des trois groupes d’un sommet, les triangles sont de la même couleur. Dans la partie supérieure, les triangles sont colorés en bleu, dans la partie inférieure gauche, les triangles sont colorés en vert, et dans la partie inférieure droite, les triangles sont colorés en magenta.
Q3: Les cinq premiers nombres qui correspondent à la régularité Xn = n2 + 1 sont :
X1 = (1)2 + 1 = 2
X2 = (2)2 + 1 = 5
X3 = (3)2 + 1 = 10
X4 = (4)2 + 1 = 17
X5 = (5)2 + 1 = 26
{2, 5, 10, 17, 26}
En savoir plus
Les formes fractales dans la nature
Un article de journal approfondi qui explore la théorie des fractales, les formes fractales en géologie et les formes fractales dans le monde vivant.
Mathématiques - Découvrir la notion de suite avec le triangle de Sierpinsky (2020)
Vidéo Youtube (4 min 47s) qui explore la notion de suite en étudiant l'évolution des triangles de Sierpinski.
À quoi les fractales servent-elles ?
Un court article décrivant la fonction des fractales.
Les fractales pour les nuls
Un article qui utilise des graphiques, des vidéos et des extraits d'informations pour expliquer de manière claire ce que sont les fractales.
Découvre les fractales avec cette expérience !
Vidéo Youtube (8min 04s) qui vous montre comment vous pouvez expérimenter la fabrication de fractales avec quelques ingrédients de chez vous.
Les Fractales
Cet article présente quelques exemples de fractales uniques dans la nature.
Références
Acuna, J. A. and Y. C. Yortsos (1995). Application of Fractal Geometry to the Study of Networks of Fractures and their Pressure Transient. Water Resources Research 31 (3): 527-540
Bhattacharya, P, B.K. Chakrabart, Kamal, and D. Samanta (2009). Fractal Models of Earthquake Dynamics. arXiv.org. Retrieved from https://arxiv.org/ftp/arxiv/papers/0906/0906.1931.pdf
Cai, J, L. Zhang, Y. Ju, G. Pia and Z. Zhang (2018). An introduction to fractal-based approaches in unconventional reservoirs - Part 1. Fractals 26 (2): 1-4
Carlotto, M. J. and M. C. Stein (1990). A method for searching for artificial objects on planetary surfaces. Journal of the British Interplanetary Society 43: 209-216
Gascueña, D. (2020). Applied Fractal Geometry: from Climate Change to Cancer. Open Mind BBVA. Retreived from https://www.bbvaopenmind.com/en/science/mathematics/applied-fractal-geometry-from-climate-change-to-cancer/
Institute of Physics (2004). Physicists Use Fractals To Help Parkinson’s Sufferers. Science Daily. Retrieved from https://www.sciencedaily.com/releases/2004/02/040203232954.htm
Marion, B. (n.d.) Fractals For Dummies. Retrieved from https://brunomarion.com/fractals-for-dummies/
MITK12Videos. (11 June 2015). What Is A Fractal (and what are they good for)? [Video]. Youtube. https://www.youtube.com/watch?v=WFtTdf3I6Ug
Norimer, N.D., R.G. Haight and R.A. Leary (1994). The Fractal Forest: Fractal Geometry and Applications in Forest Science. St. Paul, MN: U.S. Department of Agriculture, Forest Service, North Central Forest Experimental Station.