Fibonacci et le nombre d’or

Enseigne lumineuse avec effet de spirale dorée (Alina Kurianova, iStockphoto)
Découvre la séquence de Fibonacci et sa relation «dorée» avec les formes dans le monde de la beauté et de la nature.
Un motif dans la nature
T’es-tu jamais demandé pourquoi les pétales de fleurs poussent comme ils le font? Pourquoi ils sont souvent symétriques ou suivent un motif radial? Il existe beaucoup de motifs différents dans la nature. Mais l’un des plus connus est le nombre d’or.

Image - Version texte
Une photographie en couleur montre une fleur pourvue de pétales blancs répartis autour de son centre jaune.
La mise au point de la fleur la plus proche est très nette. De nombreuses fleurs similaires sont floues à l’arrière-plan. Chacune est sur une mince tige verte. Elles poussent étroitement ensemble, probablement dans la nature.
Le savais-tu?
Le nombre d’or a de nombreux noms différents. La section dorée, la proportion dorée et la divine proportion n’en sont que quelques-uns. Les gens recherchent et observent ce motif depuis des milliers d’années!
La séquence de Fibonacci
Alors d’où vient ce « nombre d’or »? Il est basé sur une séquence de nombres que les mathématiciens du monde entier étudient depuis environ 300 ans avant notre ère.
C’est à cette époque qu’ Acharya Pingala, un ancien poète et mathématicien indien, a écrit au sujet d’un motif de syllabes courtes et longues dans les lignes de la poésie sanskrite. Ce motif se traduit par une séquence de nombres portant le nom de mātrāmeru.
La même séquence a été nommée la séquence de Fibonacci environ 1 500 années plus tard. C’est là, vers l’an 1202, que le mathématicien italien Leonardo Bonacci a écrit à ce sujet dans son livre Liber Abaci. Fibonacci et ses écrits ont été importants pour le développement des mathématiques en Europe. Il a aidé à introduire le système de numération hindou-arabe ou indo-arabe à de nombreuses personnes en Occident. Ce système était beaucoup plus facile que les chiffres romains utilisés en Italie à l’époque.
Le savais-tu?
Les chiffres hindous-arabes ou indo-arabes sont le même système de nombres que nous utilisons de nos jours! Les symboles pour 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9 se sont développés en Inde et se sont répandus au Moyen-Orient et en Afrique du Nord. Les mathématiciens, y compris al-Khwarizmi et al-Kindi, ont d’abord introduit le système en Europe. Mais il a ensuite été popularisé par Fibonacci.
Dans Liber Abaci, Fibonacci a écrit à propos de quelque chose qu’on appelle le problème des lapins. Il l’expose ainsi :
Un homme a placé un couple de lapins dans un lieu entouré d’un mur. Combien de couples de lapins peuvent être produits à partir de ce couple en un an si l’on suppose que chaque couple engendre chaque mois un nouveau couple, lequel devient productif à partir du deuxième mois?
(p. 283-284, traduit du latin original)
À la fin, cet endroit clos serait bientôt rempli de lapins sautillants! Mais comment leur nombre augmenterait-il exactement? Fibonacci a écrit une série de nombres pour résoudre le problème :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1 597, 2 584, 4 181, …
Il n’y a aucun lapin le premier mois. Le deuxième mois, un couple de lapins s’installe, mais ils n’ont pas de bébé pendant les deux premiers mois. Au quatrième mois, une nouvelle paire de lapins est née! Et une autre au cinquième. Au sixième mois, les première et deuxième paires auront une paire de bébés chaque mois.
Ces nombres augmentent rapidement! Mais as-tu remarqué le motif? Après 0 et 1, chaque nouveau nombre est la somme des deux nombres qui précèdent. C’est la séquence de Fibonacci. Les nombres individuels dans cette séquence sont appelés nombres de Fibonacci.
Question 1
Quel nombre vient après 4 181 dans la séquence ci-dessus?
Le savais-tu?
« Fibonacci » était le surnom de Leonardo Bonacci. Il signifie « fils de Bonacci » en italien. Guglielmo Bonacci était un marchand et un fonctionnaire des douanes italiennes. Leonardo a voyagé avec lui en Algérie, où il a étudié le calcul. Plus tard, Fibonacci a travaillé et étudié les systèmes de nombres en Égypte, en Syrie, en Grèce, en Sicile et en Provence.
La suite de Fibonacci peut également être exprimée à l’aide de cette équation :
Fn = F(n-1) + F(n-2)
où n est supérieur à 1 (n > 1).
La séquence devient plus intéressante lorsque l’on divise chaque nombre par celui qui le précède.
Par exemple: 1÷1, 2÷1, 3÷2, 5÷3, 8÷5, 13÷8 et 21÷13.
Pour ces exemples, les réponses seraient: 1,000 ; 2,000 ; 1,500 ; 1,667 ; 1,625 et 1,615. Regarde ces nombres dans le graphique à barres ci-dessous. Les barres ont des hauteurs différentes, mais à mesure que chaque ensemble de nombres devient plus grand, la réponse se rapproche de plus en plus de la même ligne pointillée.
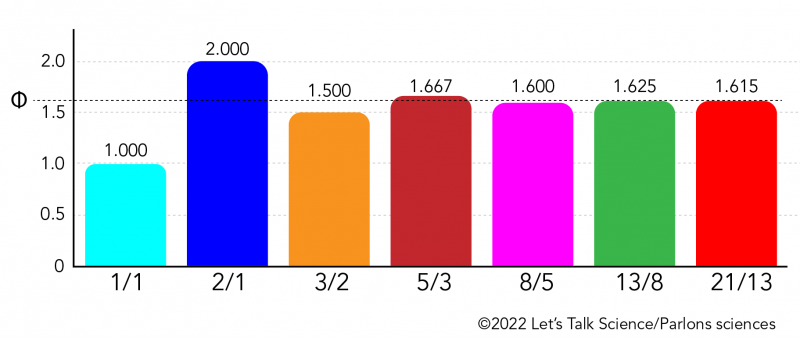
Image - Version texte
Une ligne pointillée s'étend sur le graphique, au niveau de 1,618033988749895... Elle est étiquetée avec le symbole Phi représenté par un cercle avec une ligne verticale passant par le centre.
Question 2
Quelle est la prochaine paire de nombres que tu pourrais ajouter au graphique ci-dessus? Quelle serait la valeur de ce rapport?
La ligne pointillée est marquée du symbole Φ. C’est la 21e lettre de l’alphabet grec, phi. En mathématiques, phi représente un nombre qui commence par 1,618033988749895… Et qui continue indéfiniment sans se répéter! C’est l’une des raisons pour lesquelles phi est un nombre irrationnel.
Le savais-tu?
Un nombre irrationnel est un nombre réel qui ne peut être écrit comme une simple fraction. Par exemple, 1,5 peut être écrit comme 3÷2. Mais tu ne peux pas faire cela avec phi. Le nombre pi (3,14159265358…) est aussi un nombre irrationnel.
Le nombre d’or
Le nombre d’or n’est pas le même que phi, mais il s’en rapproche! Le nombre d’or est une relation entre deux nombres qui se trouvent l’un à côté de l’autre dans la séquence de Fibonacci. Lorsque tu divises le plus grand par le plus petit, tu obtiens une réponse proche de phi. Plus tu avances le long de la séquence de Fibonacci, plus les réponses se rapprochent de phi. Mais la réponse n’égalera jamais phi exactement. C’est parce que phi ne peut pas être écrit comme une fraction. Il est irrationnel!
Le nombre d’or peut aussi être illustré à l’aide de deux quantités, comme les longueurs de deux segments de ligne. Examine les lignes ci-dessous. Les lignes bleue et verte ont le nombre d’or. En effet, la longueur de la ligne bleue plus longue, divisée par la longueur de la ligne verte plus courte, est la même que la longueur des deux lignes additionnées (illustrées en noir) et divisée par la longueur de la ligne bleue. En d’autres termes, deux quantités ont le nombre d’or si leur rapport est le même que le rapport de leur somme sur la plus grande des deux quantités.
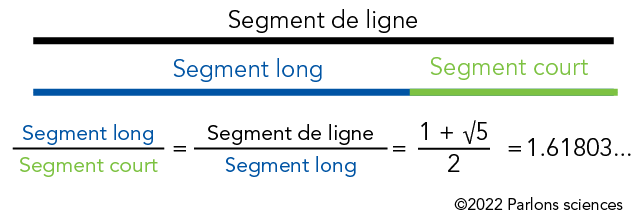
Image - Version texte
L’illustration en couleur montre des segments de ligne et une équation mathématique.
En haut se trouve une longue bande noire étiquetée «Segment de ligne». En dessous se trouve une bande bleue plus courte étiquetée «Segment long». À droite, une bande verte encore plus courte est étiquetée «Segment court». Lorsqu’elles sont placées bout à bout, les bandes bleue et verte ont la même longueur que la bande noire. L’équation se trouve sous cette illustration. À gauche, les mots «Segment long» en bleu sont divisés par les mots «Segment court» en vert. À droite, on trouve un signe d’égalité. Ensuite, les mots «Segment de ligne» en noir sont divisés par les mots «Segment long» en bleu. Cette division est suivie d’un autre signe d’égalité. Ensuite, 1 + la racine carrée de 5 est divisé par 2. Cette opération est suivie d’un autre signe d’égalité. À droite, la réponse est 1,61803...
Un rectangle d’or fonctionne de la même manière. Mais les quantités sont des formes plutôt que des lignes. Regarde le diagramme ci-dessous. Le rectangle a un côté long égal à a + b et un côté court égal à a. Il s’agit de toute la zone colorée du diagramme.
Imagine que tu coupes une section carrée en utilisant une ligne. Le carré est montré en bleu. Chacun de ses côtés est égal au côté le plus court du rectangle d’origine, ou a.
Mais regarde le plus petit rectangle restant en rose. Il a le même rapport des longueurs latérales que le rectangle d’origine! Même s’il est plus petit, il peut être divisé de la même manière que le premier.
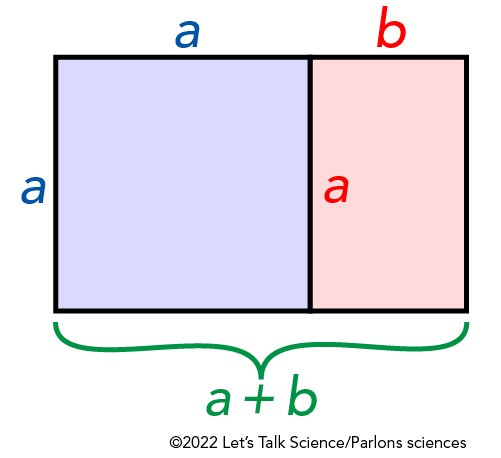
Image - Version texte
L’illustration montre un diagramme en couleur d’un rectangle divisé en un carré violet pâle et un plus petit rectangle rose.
Les côtés supérieur et gauche du carré sont chacun marqués d’un a bleu, en minuscule et italique. Le côté supérieur du plus petit rectangle est marqué d’un b rouge, en minuscule et italique. Le côté long de gauche est marqué d’un a, en rouge et italique. Tout le côté inférieur du plus grand rectangle est étiqueté a + b, en vert et italique.
Le rapport entre les côtés a et b est Φ ou 1,618... Tu peux voir ceci écrit comme une équation ci-dessous :
On peut développer ce motif en ajoutant un carré plus grand au côté long (a + b) du rectangle. Ce carré, combiné aux formes précédentes, donne un nouveau rectangle plus grand. En procédant ainsi encore et encore, tu peux créer un motif croissant, comme le diagramme ci-dessous.
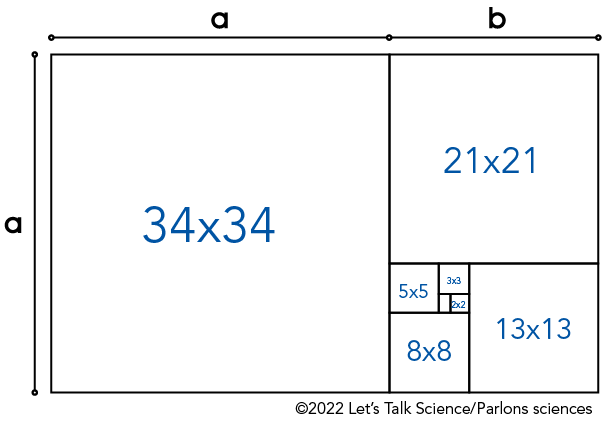
Image - Version texte
L’illustration en noir et blanc montre un rectangle divisé en carrés et en rectangles plus petits. Ceux-ci deviennent plus petits à mesure qu’ils se déplacent autour de l’image, vers un point situé dans le quadrant inférieur droit. Chaque carré est étiqueté avec des mesures.
Le côté court du plus grand rectangle est étiqueté a. La première section du côté long est également étiquetée a. La deuxième section, qui forme le côté court d’un plus petit rectangle à l’intérieur du premier, est étiquetée b.
À l’intérieur du rectangle, le plus grand carré est étiqueté 34 × 34. À droite de ce carré se trouve un rectangle vertical. Celui-ci est divisé en un carré étiqueté 21 × 21 et un autre rectangle horizontal plus petit.
Le troisième rectangle est à nouveau divisé. Le carré de droite est étiqueté 13 × 13. Le rectangle vertical est à nouveau divisé en un carré étiqueté 8 × 8 et un rectangle horizontal qui est à nouveau divisé.
Le carré suivant est étiqueté 5 × 5. À sa droite, un autre rectangle vertical contient un carré étiqueté 3 × 3 et un plus petit rectangle horizontal, qui contient à son tour un carré étiqueté 2 × 2. Le plus petit carré n’est pas étiqueté, mais ce motif semble se perpétuer, se divisant en formes de plus en plus petites.
Question 3
Quelle serait la taille du prochain carré, pour continuer à développer le motif dans le diagramme ci-dessus?
On peut développer le rectangle d’or encore davantage en ajoutant une ligne qui forme un quart de cercle dans chaque carré.
Examine le diagramme ci-dessous. Les lignes incurvées se connectent pour former une spirale. C’est ce qu’on appelle une spirale de Fibonacci. Chaque carré est aussi étiqueté avec un nombre correspondant à la longueur de ses côtés. Ce sont les mêmes nombres que ceux de la séquence de Fibonacci!
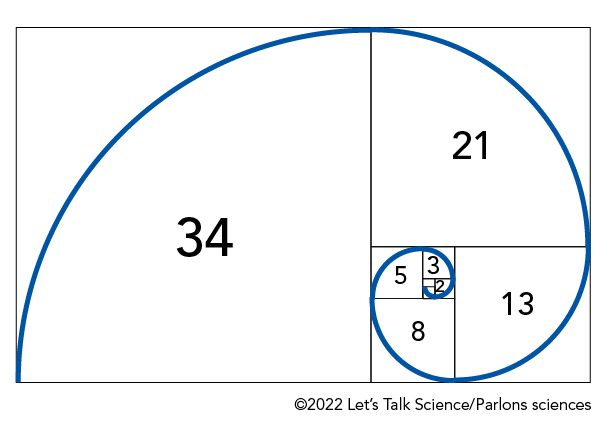
Image - Version texte
L’illustration en noir et blanc montre un rectangle divisé en carrés et en rectangles plus petits, sur lequel une ligne spirale de couleur bleue est superposée.
Le plus grand rectangle est divisé en plusieurs formes plus petites. La plus grande, à gauche, est un carré marqué du chiffre 34. La ligne bleue superposée s’incurve du coin inférieur gauche au coin supérieur droit, formant un quart de cercle.
À droite du carré se trouve un rectangle vertical. Il est divisé en un carré marqué du chiffre 21 et un autre rectangle horizontal plus petit. Un autre quart de cercle est superposé sur le carré marqué du chiffre 21, depuis le coin supérieur gauche au coin inférieur droit.
Le troisième rectangle est à nouveau divisé. Le carré de droite est marqué du chiffre 13. Une ligne bleue incurvée du coin supérieur droit au coin inférieur gauche y est superposée.
Le rectangle vertical est à nouveau divisé en un carré marqué du chiffre 8 et un rectangle horizontal qui est à nouveau divisé. La ligne bleue continue de s’incurver sur ces formes.
Le carré suivant est marqué du chiffre 5. À sa droite, un autre rectangle vertical contient un carré marqué du chiffre 3 et un plus petit rectangle horizontal, qui contient à son tour un carré marqué du chiffre 2. La ligne bleue continue de s’incurver sur ces formes.
Le plus petit carré n’est pas étiqueté, mais c’est l’endroit où la spirale bleue se termine en une courbe serrée. Le motif semble se perpétuer, se divisant en formes de plus en plus petites, la spirale devenant de plus en plus serrée.

Comment fabriquer une spirale de Fibonacci (©2022 Parlons sciences).
Image - Version texte
Voici un GIF animé d’une spirale qui s’agrandit avec des carrés de plus en plus grands de différentes couleurs.
Le premier carré est minuscule et bleu, superposé d’une ligne blanche incurvée du coin inférieur gauche au coin supérieur droit. Le deuxième carré apparaît au-dessus. Il est vert et beaucoup plus grand, et la ligne s’incurve du coin inférieur droit vers le coin supérieur gauche. Le troisième carré est rouge et encore plus grand. Il apparaît à gauche des autres carrés, et la ligne s’incurve du coin supérieur droit vers le coin inférieur gauche. Le quatrième carré apparaît en violet sous les autres carrés, avec une ligne allant du coin supérieur gauche au coin inférieur droit. Le cinquième carré est orange et apparaît à droite, avec une ligne allant du coin inférieur gauche au coin supérieur droit. Le sixième carré apparaît au-dessus des autres, en rose, avec une ligne allant du coin inférieur droit au coin supérieur gauche. Le dernier carré est si grand qu’il occupe plus de la moitié de la surface de l’image et remplit tout l’espace à gauche du reste des carrés. Il est bleu avec une ligne incurvée qui le traverse du coin supérieur droit vers le coin inférieur gauche.
Lorsque tous les carrés sont réunis, les lignes courbes qui les traversent forment une spirale. Cette spirale se développe à partir d’un minuscule carré blanc dans la section inférieure droite de l’image.
Les spirales de Fibonacci dans la nature
Tu te souviens de ces pétales de fleurs? Ils aident à attirer les pollinisateurs vers le centre de la fleur où se trouve le pollen - comme un œil-de-bœuf. C’est pourquoi de nombreuses fleurs ont évolué pour faire pousser des pétales selon une spirale de Fibonacci autour de leurs centres. Chaque nouveau pétale pousse à environ 137,5 degrés du précédent. Il s’agit de 1 ÷ phi x 360 (degrés totaux dans le cercle). Ou encore tu peux imaginer un cercle divisé en deux lignes courbes. L’arc de la plus longue ligne et l’arc de la plus courte ligne ont le nombre d’or. C’est ce qu’on appelle l’angle d’or. En fait, si tu peux compter tous les pétales sur une fleur, Tu trouverais souvent un nombre de Fibonacci!

Image - Version texte
Cinq photographies en couleur montrent des fleurs différentes et uniques, disposées en rangées et étiquetées avec leur nombre de pétales.
La première fleur a 3 larges pétales blancs pointus et 3 feuilles vertes plus petites. La deuxième a 5 pétales ronds pourpre bleuâtre autour d’un petit centre jaune. La troisième a 8 pétales en forme d’amande qui sont rose foncé près du centre et blancs aux extrémités. La quatrième a 13 pétales jaunes longs et étroits avec des extrémités incurvées. La cinquième a 21 longs pétales étroits et mauves vifs autour d’un centre violet plus foncé.
Mais ce ne sont pas seulement les pétales qui adoptent ce motif. D’autres parties de la plante suivent également la séquence de Fibonacci. Les graines ont besoin de suffisamment d’espace pour pousser correctement. Regarde le tournesol ci-dessous. Les graines sont rassemblées au centre de la fleur selon un motif très familier!

Image - Version texte
Cette image est une photographie en couleurs du centre d’un tournesol, sur lequel est superposée une spirale bleue.
La fleur a des pétales jaune vif. Son centre est constitué de minuscules structures pointues, d’un jaune profond, densément regroupées en un cercle. La spirale montre que les structures pointues sont disposées selon un motif semblable à une spirale de Fibonacci.
Alerte aux idées fausses
Les spirales de Fibonacci et les spirales dorées ne sont pas les mêmes. Une spirale de Fibonacci est faite de carrés qui augmentent en taille. Mais une spirale dorée résulte de l’imbrication de rectangles dorés de plus en plus petits dans un grand rectangle doré.
Le nombre d’or peut aussi être utilisé avec d’autres formes. Il est possible de trouver des nombres d’or dans des motifs impliquant des cercles, des triangles, des pentagones et d’autres formes.
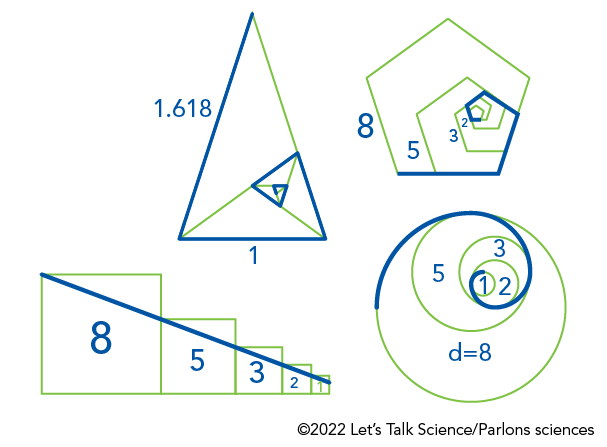
Image - Version texte
Voici un diagramme de triangles, de pentagones, de carrés et de cercles qui se croisent et sur lesquels des lignes bleues sont superposées.
Le plus grand triangle est aigu et contient sept autres triangles plus petits. Son côté gauche est recouvert d’une ligne bleue, marquée 1,618. La ligne bleue tourne le coin et continue sur son côté inférieur, marqué du chiffre 1. Ce triangle est divisé en un triangle isocèle et un triangle scalène. Le triangle scalène est à son tour divisé en un autre triangle aigu et un autre triangle isocèle. La ligne bleue continue autour du côté long, puis sur le côté court du triangle aigu. Ce triangle est à nouveau divisé en un autre triangle aigu et un autre triangle isocèle. La ligne bleue continue le long de la base du triangle aigu, qui est à nouveau divisé en un autre triangle aigu et un autre triangle isocèle. La ligne bleue continue le long de cette base et le triangle est à nouveau divisé. La ligne bleue se termine en formant un angle serré le long de la base du plus petit triangle aigu. Au total, la ligne bleue forme une sorte de spirale, avec une série d’angles aigus et de segments droits qui deviennent de plus en plus courts et se rapprochent d’un point situé dans la section inférieure droite du plus grand triangle.
Le plus grand pentagone est étiqueté 8. Son côté inférieur est recouvert d’une ligne bleue. À l’intérieur de celui-ci, un pentagone plus petit est étiqueté 5 et la ligne bleue continue le long d’un de ses côtés. À l’intérieur de ce pentagone se trouvent des pentagones plus petits marqués des chiffres 3 et 2, où la ligne continue le long de l’un de leurs côtés. Deux pentagones encore plus petits ne comportent aucune étiquette, mais ils suivent le même motif. Tous les segments de la ligne bleue forment une spirale constituée d’angles obtus et de segments droits qui raccourcissent et se rapprochent d’un point situé dans la section inférieure droite du plus grand pentagone.
Le plus grand carré est étiqueté 8, tandis qu’un plus petit, qui lui est accolé à droite, est étiqueté 5. Une ligne bleue est tracée depuis le coin supérieur gauche du grand carré vers le coin supérieur gauche du petit carré, formant une pente vers la droite. Des carrés de plus en plus petits, étiquetés 3, 2 et 1, suivent le même motif, et la ligne bleue continue à descendre en ligne droite jusqu’au plus petit carré, situé à l’extrême droite.
Le plus grand cercle est étiqueté d = 8. Une ligne bleue couvre la partie supérieure gauche de la circonférence. À l’intérieur de celle-ci, des cercles plus petits sont étiquetés 5, 3, 2 et 1. La ligne bleue continue le long d’une partie de la circonférence de chaque cercle, formant une spirale. Celle-ci s’enroule jusqu’à son plus petit point dans la section supérieure droite du plus grand cercle.
Alors, les plantes font des maths ! Plutôt intelligent, non?
Réponses :
Question 1
Quel nombre vient après 4 181 dans la séquence ci-dessus?
6 765
Question 2
Quelle est la prochaine paire de nombres que tu pourrais ajouter au graphique ci-dessus? Quelle serait la valeur de ce rapport?
34/21; 1,619
Question 3
Quelle serait la taille du prochain carré, pour continuer à développer le motif dans le diagramme ci-dessus?
55x55
En savoir plus
KEZAKO - La Suite de Fibonacci (2013)
Cette vidéo (4 min 37 s) de Anthony Ghelfo explique brièvement Fibonacci et Le problème des lapins.
Suite de Fibonacci (2020)
Cette vidéo (1 min 8 s) de Éditions Larousse explique comment l'effectif théorique d'une population de lapins, issue d'un seul couple, décrit cette suite.
Introduction aux nombres rationnels et irrationnels (2014)
Cette vidéo (6 min 40 s) de KhanAcademyFrancophone explique comment faire la différence entre les nombres rationnels et les nombres irrationnels avec quelques exemples d'irrationnels célèbres.
Références
Be Smart (2021). The Golden Ratio: Is It Myth or Math? YouTube.
Carney-Gies, F. (2023, August 9). Fibonacci. Encyclopedia Britannica.
Cuemath. (2020, September 17). Acharya Pingala.
The Editors of Encyclopedia Britannica. (2023, September 14). Hindu-Arabic numerals. Encyclopedia Britannica.
Haglund, C. (2023, May 3). Flowers & the Fibonacci Sequence. Montana Natural History Center.
Huffman, C. J. (n.d.). Mathematical Treasure: Fibonacci's Liber Abaci. Mathematical Association of America.
Mann, A. (Nov 25, 2019). Phi: The Golden Ratio. LiveScience.
Math Is Fun (n.d.). Nature, The Golden Ratio, and Fibonacci too...
Phyllotaxis (n.d.). Fibonacci Numbers - Golden Angle.
Reich, L. (2013, February 20). Nature follows a number pattern called Fibonacci. Phys.org.
Wikipedia. Pingala.