Les mathématiques qui font fonctionner le GPS

As-tu déjà ouvert une application de cartographie sur ton téléphone ou indiqué ton emplacement sur les réseaux sociaux?

Tu peux faire tout cela sur ton téléphone, car il peut accéder au système de Géolocalisation Par Satellite ou GPS. Ce système de satellites nous aide à savoir où nous nous situons et à nous rendre là où nous voulons aller. 

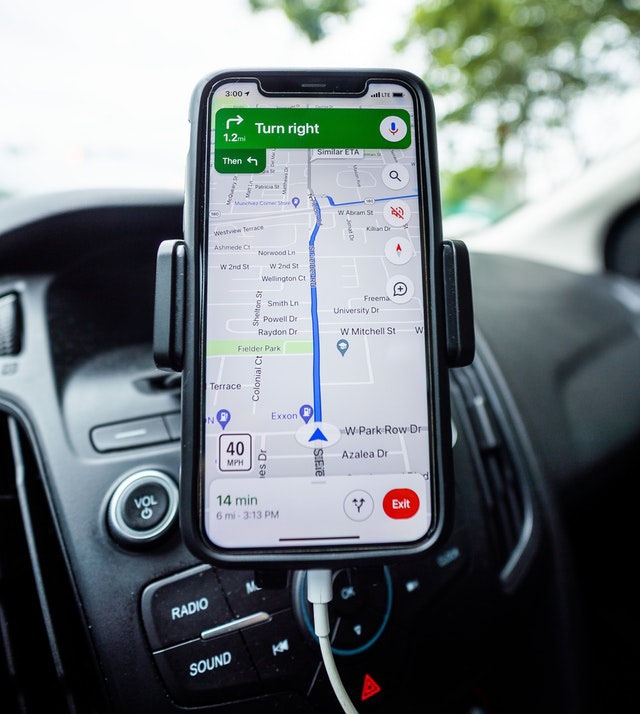
Image – Version texte

La photo montre un téléphone intelligent fixé au tableau de bord d’une voiture. Sur le téléphone, tu peux voir une carte indiquant l’itinéraire à suivre pour se rendre à un endroit.

Les GPS sont utiles dans nos téléphones, mais ils sont aussi importants pour les navires, les avions, les ambulances et bien plus encore. Cependant, les mathématiques, la science et l’histoire de cette technologie demeurent un mystère pour beaucoup d’entre nous. Comment un système qui s’intègre à un téléphone intelligent peut-il localiser instantanément ton emplacement?

L’histoire du GPS

Dans les années 1950, des chercheuses et des chercheurs ont développé le premier système de navigation par satellite à des fins militaires. Dans les années 1980, après plusieurs décennies d’améliorations, les GPS ont commencé à être utilisés par le grand public. Le système est devenu pleinement fonctionnel en 1994. Le gouvernement des États-Unis possède et entretient le système de Géolocalisation Par Satelliteque nous utilisons partout en Amérique du Nord.

Des scientifiques de nombreux domaines différents ont contribué au développement du GPS. Gladys Mae West est l’une des mathématiciens et mathématiciennes qui ont rendu ce système possible. Elle a créé un modèle mathématique incroyablement détaillé de la forme de la Terre. Ce modèle permet au GPS de localiser avec précision des emplacements sur Terre.

Image – Version texte

L’image est en fait une photo en noir et blanc de Sam Smith et Gladys West. Sam Smith est un homme blanc d’âge moyen en complet veston. Gladys est une femme noire d’âge moyen, également en tenue de ville. Ils se tiennent debout dans une salle devant un bureau couvert de documents. Stylo à la main, Gladys pointe quelque chose sur l’une des feuilles de papier. Sam regarde ce qu’elle lui montre. Un très grand globe terrestre sur un piédestal se trouve à côté de Gladys.

Attention aux fausses idées!

La Terre n’est pas une sphère parfaite. Elle présente des reliefs et Gladys Mae West a contribué à créer une représentation plus réaliste d’elle.

Roger Easton, Ivan Getting et Bradford Parkinson (en anglais) ont également joué un rôle clé dans le développement du GPS. Ces physiciens et ingénieurs ont élaboré des moyens de localiser les satellites et les emplacements sur la Terre.

Comment fonctionnent les GPS?

Avant le développement des GPS, les gens utilisaient plusieurs techniques de navigation différentes. Les marins utilisaient souvent la position des étoiles dans le ciel pour savoir dans quelle direction aller.

Les techniques de navigation aident les gens à trouver leur latitude et leur longitude. Les lignes de longitude vont du nord au sud. La ligne de longitude 0º passe par Greenwich, en Angleterre. Les lignes de latitude vont d’est en ouest. La ligne de latitude 0º est l’Équateur. En sachant ta longitude et ta latitude, tu peux connaître ta position sur le globe.

Plutôt que de se fier aux étoiles, les GPS se servent des satellites pour déterminer la longitude et la latitude d’un emplacement. Les GPS s’appuient sur un réseau de plus de 30 satellites. Ces satellites font le tour de la Terre deux fois par jour. Les centres de contrôle sur Terre veillent au bon fonctionnement de ces satellites.

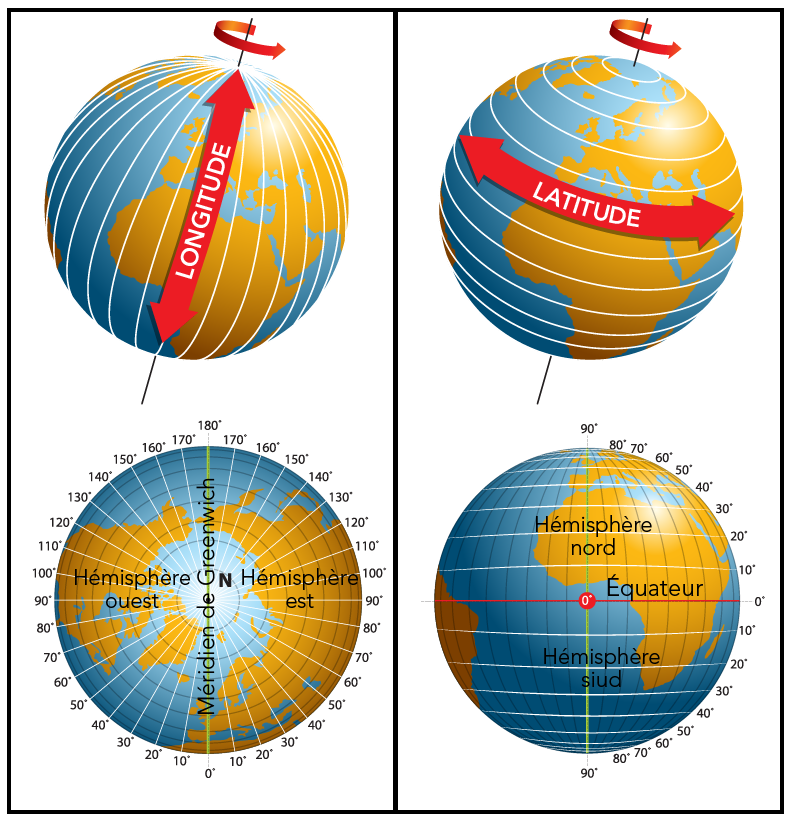
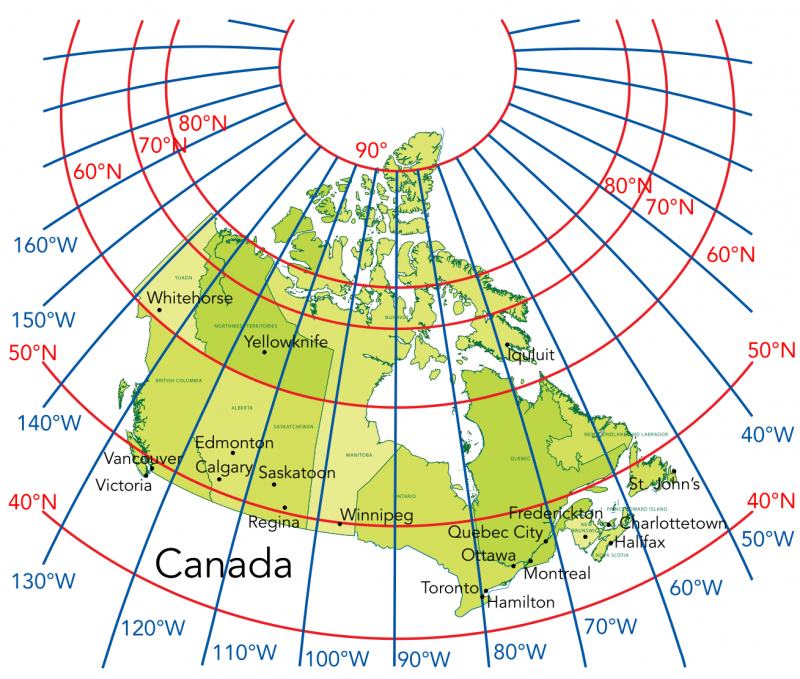
Image – Version texte

Voici une illustration en couleur de la Terre dans l’espace. Environ 20 petits satellites orbitent autour de la Terre. La direction de leur mouvement est indiquée par des sillons blancs derrière chaque satellite.

Ces satellites communiquent avec des récepteurs. Les récepteurs peuvent se retrouver dans ton téléphone intelligent, ta voiture ou ton ordinateur. Les récepteurs reçoivent des signaux des satellites. Les signaux se déplacent à la vitesse de la lumière. Ce qui équivaut à environ 300 000 000 de mètres par seconde).

Une composante essentielle du signal est la précision du temps. Les satellites connaissent l’heure grâce à des horloges atomiques incroyablement précises.

Image – Version texte

L’illustration montre un satellite et un téléphone portable.
Le satellite se trouve dans la partie supérieure gauche de l’image. Des lignes en demi-cercle rayonnent vers le bas indiquant que le satellite transmet un signal vers la Terre. Le téléphone intelligent se trouve dans la partie inférieure et centrale de l’image. Des lignes en demi-cercle rayonnent vers le haut indiquant que le téléphone envoie un signal au satellite. Une petite image d’une punaise de carte et une voiture sont reliées par une ligne pour indiquer que le téléphone utilise les informations pour les applications de cartographie et les systèmes de navigation des véhicules.

 Un récepteur utilise la formule suivante :

Distance = vitesse du signal x temporisation de signal

La vitesse du signal est la vitesse de la lumière (environ 300 000 000 m/s). La temporisation de signal est le temps que met le signal à voyager du satellite jusqu’au récepteur. En multipliant ces deux nombres, on obtient la distance entre le satellite et le récepteur.

Par exemple, imagine qu’un signal met 0,005 seconde à voyager depuis un satellite jusqu’à ton téléphone.

Distance = 300 000 000 m/s x 0,005 s = 1 500 000 mètres

Nous savons donc que le satellite se trouve à 1,5 million de mètres ou 1500 kilomètres du récepteur.

Le savais-tu?

Les GPS s’appuient sur la théorie de la relativité d’Albert Einstein. Les informations temporelles transmises par les satellites sont ajustées pour tenir compte de la relativité. C’est ce qui ajoute à la précision du système.

Cependant, savoir à quelle distance tu te situes par rapport à un satellite ne te donne pas ta position. Pour y parvenir, les GPS s’appuient sur la trilatération.

La trilatération

La trilatération est un moyen de situer un point d’après la mesure de trois autres points qui le séparent. Pour fonctionner de cette manière, plusieurs satellites doivent se connecter au récepteur. On calcule la distance entre le récepteur et plusieurs satellites. La trilatération est une méthode qui consiste à utiliser ces mesures de distance pour localiser un emplacement.

Attention aux fausses idées!

Le GPS s’appuie sur la trilatération et non sur la triangulation. La trilatération implique de mesurer des distances. Elle est parfois confondue avec la triangulation qui implique la mesure d’angle.

Voici un exemple simple du fonctionnement de la trilatération. Imagine que tu te trouves sur un terrain de soccer. Imagine ensuite que tu essaies de trouver un ballon sur le terrain en te basant sur les indices suivants.

1. Le ballon est à 20 m du coin inférieur droit.
2. Il est aussi à 40 m du centre du terrain.
3. Enfin, le ballon est à 15 m du centre du but de gauche.

Avec ces trois indices, arrives-tu à localiser le ballon de soccer?

Tout d’abord, nous pouvons dessiner un cercle d’un rayon de 20 mètres autour du coin inférieur droit. Nous savons maintenant que le ballon se trouve quelque part SUR la ligne du cercle bleu.

Image – Version texte

Voici une illustration d’un terrain de soccer. En bas à droite de l’illustration, un cercle bleu a été tracé. Son centre se trouve au coin inférieur droit du terrain de soccer. Le rayon du cercle est de 20 mètres.

Ensuite, nous pouvons dessiner un cercle avec un rayon de 40 mètres à partir du centre du terrain. Maintenant, quels sont les deux endroits possibles où le ballon pourrait se trouver? N’oublie pas que le ballon se trouve sur la ligne du cercle.

Tu as probablement compris qu’il s’agit des deux endroits où les cercles se croisent.

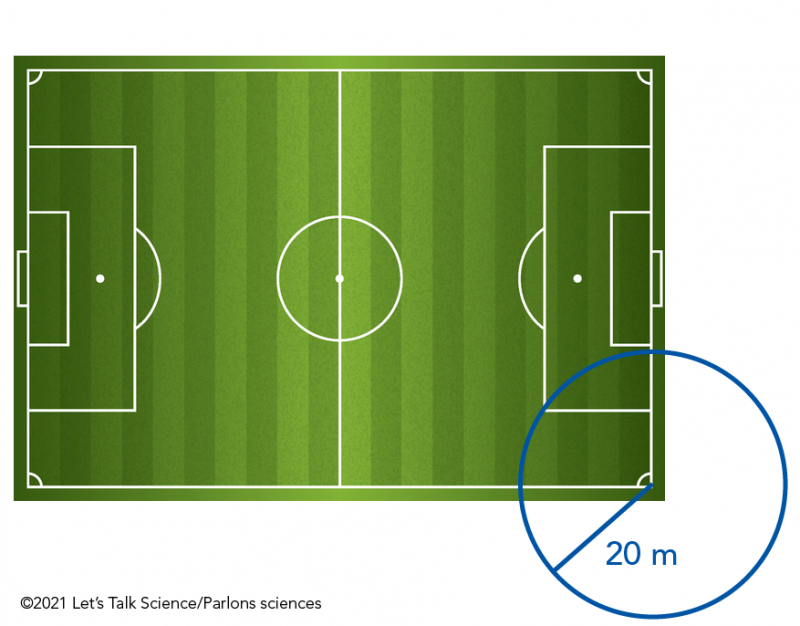
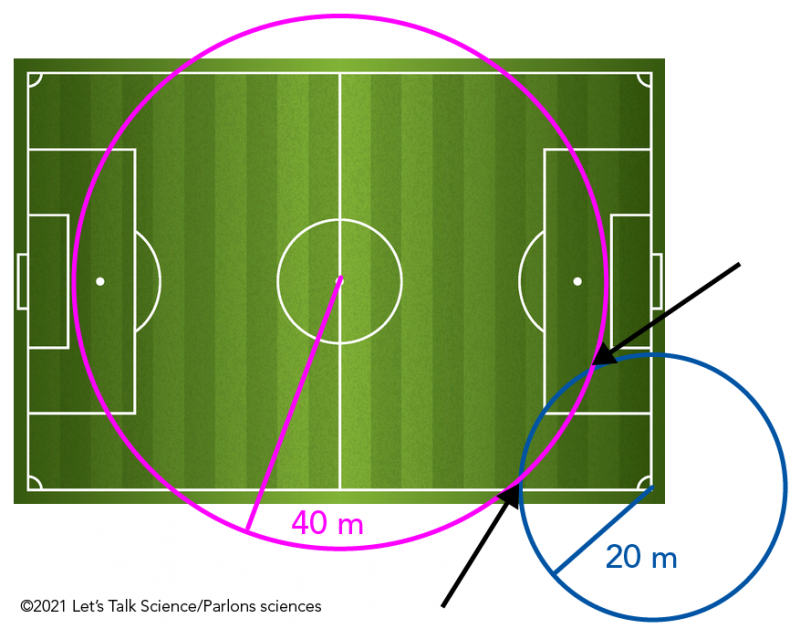
Image – Version texte

Voici une illustration d’un terrain de soccer. En bas à droite de l’illustration, un cercle bleu a été tracé. Son centre se trouve au coin inférieur droit du terrain de soccer. Le rayon du cercle est de 20 mètres. Au centre de l’illustration, un cercle rose a été tracé. Son centre se situe au centre du terrain de soccer. Le rayon du cercle est de 40 mètres.

Pour savoir laquelle de ces deux positions est la bonne, nous avons besoin d’un troisième indice. Une fois que nous aurons dessiné le troisième cercle, nous saurons exactement où se trouve le ballon.

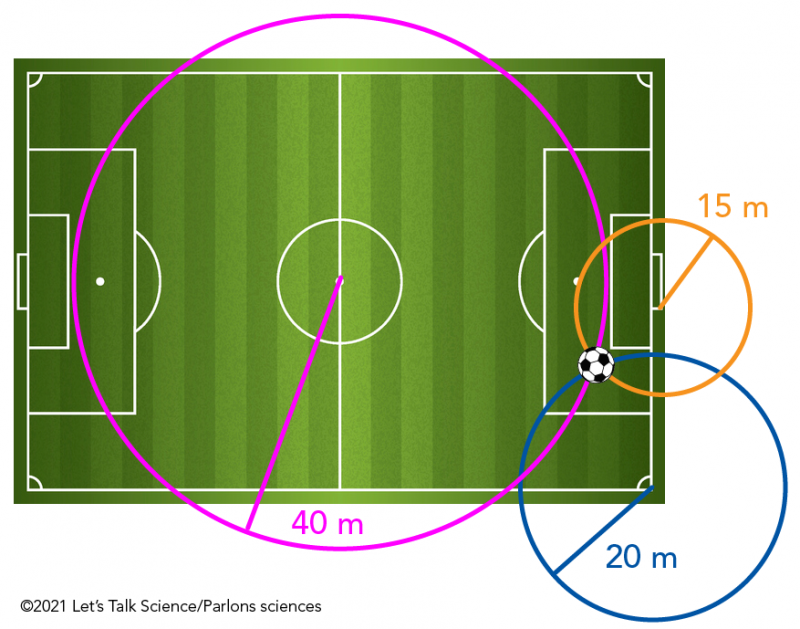
Image – Version texte

Voici une illustration d’un terrain de soccer. En bas à droite de l’illustration, un cercle bleu a été tracé. Son centre se trouve au coin inférieur droit du terrain de soccer. Le rayon du cercle est de 20 mètres. Au centre de l’illustration, un cercle rose a été tracé. Son centre se situe au centre du terrain de soccer. Le rayon du cercle est de 40 mètres. Au centre droit de l’illustration, un cercle orange a été tracé. Son centre se situe dans la zone de but. Le rayon du cercle est de 15 mètres. Une image d’un ballon de soccer a été placée à l’endroit où les contours des trois cercles se croisent.

L’exemple du ballon de soccer illustre une trilatération en 2D. La trilatération par satellites implique la même méthode. En revanche, la trilatération en 3D s’appuie sur l’intersection de sphères plutôt que de cercles.

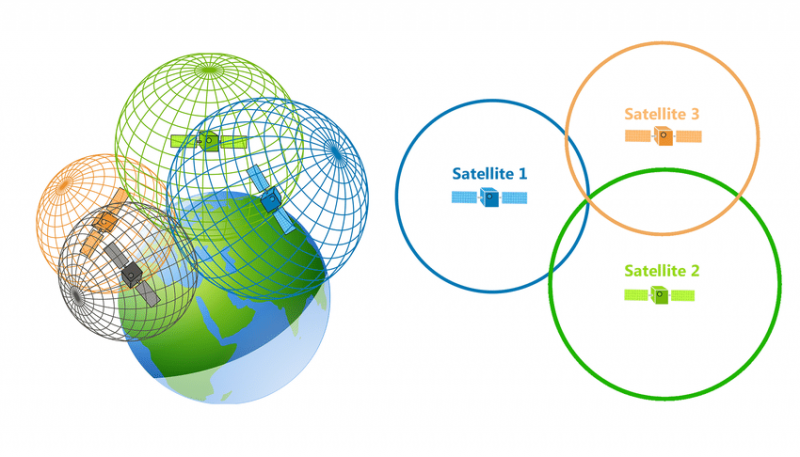
Image – Version texte

Voici une illustration de trilatération en deux et en trois dimensions.
À gauche, une image montre la Terre et quatre satellites en orbite. Les satellites sont de couleur vert, gris, orange et bleu. Chaque satellite est entouré d’une sphère de la même couleur. Les quatre sphères s’entrecroisent légèrement.
À droite, une image présente trois satellites. Les satellites sont de couleur bleu, orange et vert. Chaque satellite se trouve au centre d’un cercle de sa propre couleur. Les trois cercles s’entrecroisent en un point.

 

Visionne la vidéo ci-dessous pour en apprendre encore plus.

(Remarque : la vidéo suivante apparaît avec une vignette qui indique généralement une "vidéo cassée" sur YouTube, mais la vidéo fonctionne correctement).

Comme le montre l’exemple ci-dessus, la trilatération ne nécessite que trois satellites. Dans ce cas, pourquoi avons-nous besoin d’un quatrième satellite? Le quatrième satellite corrige les erreurs de l’horloge du récepteur. Cela ajoute à la précision du GPS. À l’heure actuelle, un téléphone intelligent doté d’un GPS peut connaître ta position à environ 5 mètres près.

De nos jours, il est normal d’utiliser la navigation par satellite au quotidien. Les applications de cartographie nous permettent de retrouver notre chemin, peu importe où nous sommes dans le monde. Nous utilisons les systèmes de localisation par satellite pour de nombreuses activités sociales, comme pour indiquer notre position géographique sur des publications ou encore la géocachette*. Au départ, les secouristes utilisaient les systèmes de localisation par satellite pour se rendre rapidement sur le lieu d’une urgence et intervenir en cas de catastrophes. Les systèmes GPS ont aussi aidé les avions à arriver à destination en toute sécurité. Les scientifiques utilisent les systèmes GPS pour prévoir la météo. Et ce ne sont que quelques-unes des façons dont nous utilisons cette technologie.

La prochaine fois que tu utiliseras un système GPS, prends une minute pour repenser à ce qui rend cette technologie possible.

*Cette page est disponible en français. Dans le coin supérieur droit, il y a un menu déroulant qui te permet de changer la langue en français.