Planifier pour des transports en commun équitables

Rame de métro TTC (ViaAmtrakGuy, Wikimedia Commons)

Rame de métro TTC (ViaAmtrakGuy, Wikimedia Commons)
Quels sont les liens avec mon programme d'études?
Découvre comment nous pouvons utiliser l'analyse spatiale pour planifier des transports publics plus équitables.
Pense à tous les endroits où les membres de ta famille se rendent au cours d'une semaine. Ils et elles peuvent aller à l'école, sur leur lieu de travail, à l'épicerie ou chez le médecin. Nos choix quotidiens sont souvent déterminés par le temps qu'il faut pour se rendre à ces endroits. Par exemple, tu n'as probablement pas envie d'aller dans une épicerie qui se trouve à 4 heures de ton domicile ! Avoir des services et des magasins proches nous fait gagner du temps et facilite nos vies.

Image - Version texte
On voit des personnes assises dans un autobus public. Au centre, un homme d'une vingtaine d'années, à la peau marron foncé et aux cheveux mi-longs, est assis à côté d'une femme d'une vingtaine d'années, à la peau marron clair et aux cheveux longs bouclés. Elle porte des lunettes à monture foncée. La femme fait des gestes avec ses mains. Les deux sourient. Un homme d'une vingtaine d'années, à la peau blanche et aux cheveux châtain clair, portant une moustache et une courte barbe, est représenté dans la rangée de sièges située devant eux. Un jeune garçon à la peau blanche pâle et aux cheveux bruns est assis près de la fenêtre dans la rangée derrière eux.
Qu'est-ce que l'analyse spatiale ?
Les urbanistes utilisent l'analyse spatiale pour prendre des décisions concernant la conception des villes. L'analyse spatiale est une façon d'interpréter les informations géographiques pour répondre à des questions. Que tu le saches ou non, tu fais une analyse spatiale chaque fois que tu regardes une carte. Par exemple, jette un coup d'œil à cette carte du métro de Toronto.
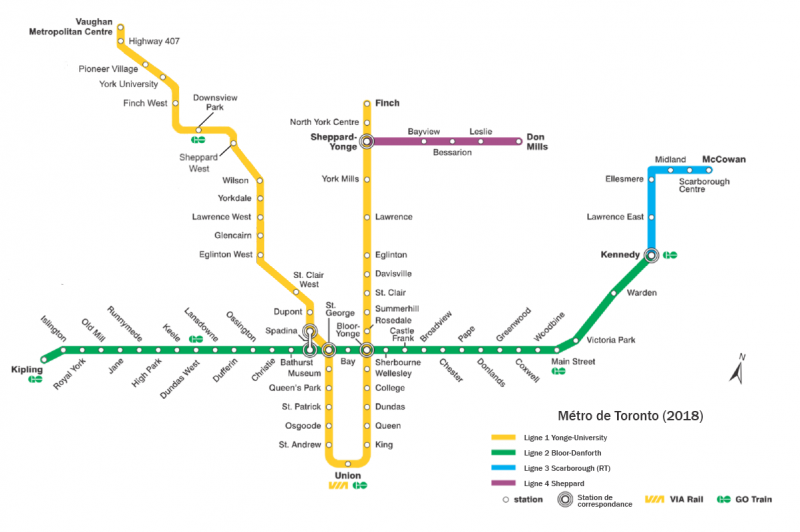
Image - Version texte
Voici une carte du réseau de métro de Toronto en 2018. Quatre lignes sont représentées. La ligne 1 est représentée en jaune. Elle forme un long U qui traverse la ville du nord au sud. La ligne 2 est représentée en vert. Elle traverse la ville d'est en ouest. Elle s'incurve vers la droite à l'extrémité est de la ligne. La ligne 3 est représentée en bleu. Elle s'étend à partir de l'extrémité est de la ligne 2. Elle va vers le nord sur une courte distance puis tourne brusquement vers la droite et s'étend sur une courte distance. La ligne 4 est représentée en violet. Elle se prolonge vers l'est à partir de l'arrêt Sheppard-Yonge de la ligne 1.
Q1: Quelle ligne faut-il prendre pour aller de la station Kipling à la station Woodbine ?
Déterminer comment se rendre d'un point à un autre sur une carte est une forme simple d'analyse spatiale. Nous utilisons des ordinateurs pour réaliser des formes plus complexes d'analyse spatiale. Les systèmes d'information géographique (SIG) relient les données à un emplacement sur une carte informatisée. Les SIG nous aident à répondre à des questions plus complexes. Par exemple, nous pouvons associer des données provenant du recensement ou de sondages sur les occupants des logements à des lieux. Le SIG nous permet ensuite de rechercher des régularités dans ces données. Voyons un exemple de la façon dont les gens utilisent les SIG pour construire des villes plus agréables à vivre.
Le savais-tu ?
Le premier système SIG informatisé a été développé au Canada dans les années 1960. Ce système permettait de suivre les ressources naturelles et l'utilisation des terres.
L'analyse spatiale en action : Le transport en commun et l'accès aux emplois à Toronto
La possibilité d'accéder aux emplois est un élément important d'une ville saine. Dans une grande ville comme Toronto, en Ontario, les transports en commun représentent souvent le moyen le plus abordable de se déplacer. L’équipe de planification chez Jacobs (en anglais) a utilisé le SIG pour étudier la question :
Quel sera l'impact des nouvelles lignes de transport en commun sur les quartiers les plus vulnérables de Toronto ?
Q2: De quelles informations aurais-tu besoin pour répondre à cette question ?
Pour répondre à cette question, ils ont dû déterminer le temps que mettent les gens pour se rendre au travail. Pour ce faire, ils ont créé une grille de points couvrant l'ensemble de Toronto.
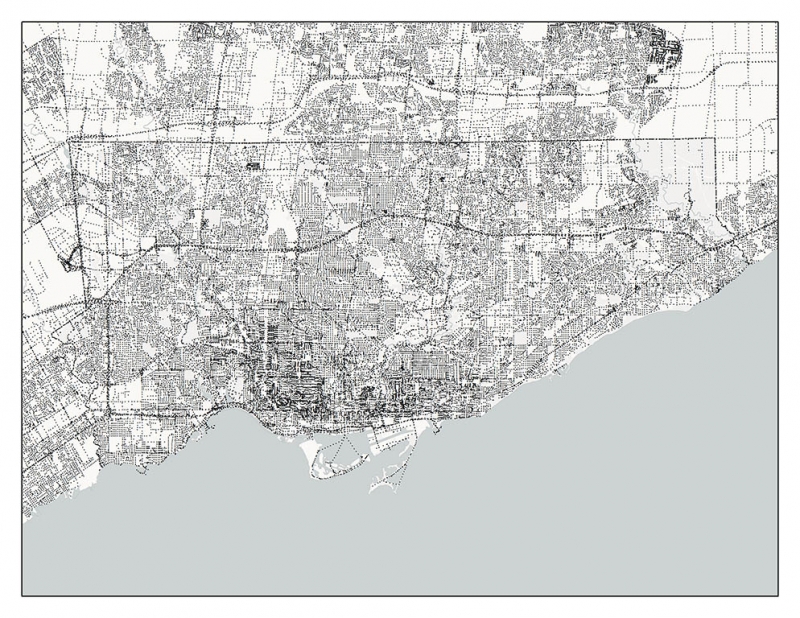
Image - Version texte
On voit ici une carte de Toronto avec les points de la grille et les réseaux utilisés dans cette analyse. Les points d'intersection de la grille sont représentés par de petits points noirs. Il y en a des milliers dans la ville. Les réseaux sont représentés par des lignes noires de différentes épaisseurs.
Ensuite, les planificateurs et planificatrices ont inclus un réseau montrant les moyens de déplacement que les personnes peuvent utiliser. Il s'agit des trottoirs, des routes, des métros et des trajets des lignes d’autobus. Ils et elles ont ainsi pu calculer le temps nécessaire à une personne pour se rendre d'un point du réseau à un autre.
Voyons comment ils et elles ont analysé les trajets menant d'un point de la grille à un autre. Si tu étais sur ce trajet, ça ressemblerait à quelque chose comme ça :
- Sortir de chez toi et marcher jusqu'au trottoir.
- Marcher le long du trottoir jusqu'à l'arrêt d’autobus.
- Monter dans le bus et voyager sur cette ligne.
- Transférer d’autobus et emprunter d'autres routes.
- Descendre de l’autobus.
- Marcher sur le trottoir et entrer dans ton école.

Image - Version texte
L'illustration en couleur d'une rue de ville montre les étapes que doit suivre une personne pour se rendre d'un point de la grille à un autre. Trois bus publics jaunes sont représentés dans la rue. Plusieurs personnes attendent à un arrêt d’autobus. D'autres personnes traversent une rue ou prennent le métro. Une plaque de rue indiquant "Main St" est visible. De grands bâtiments bleus aux fenêtres noires sont en arrière-plan.
La façon dont l'analyse voit ce voyage est :
- Passer d’un point de la grille au réseau
- Se déplacer le long du réseau en utilisant le chemin le plus court.
- Sortir du réseau et revenir à un autre point de la grille.
Examinons les calculs derrière ces étapes.
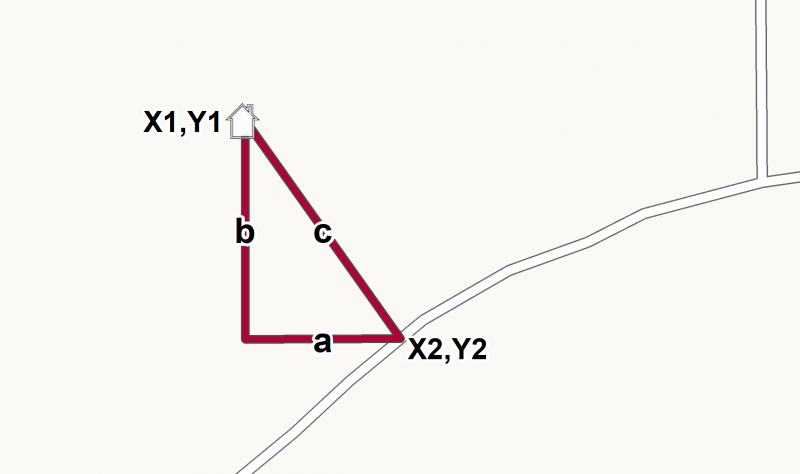
Image - Version texte
L'illustration montre comment un triangle peut être utilisé pour identifier la plus courte distance entre deux points. En haut à gauche, il y a un petit dessin au trait gris représentant une maison. La maison se trouve au sommet le plus haut relié à l'hypoténuse (ou plus long côté) d'un triangle rectangle. Une route traverse l'image sous le triangle. Un point de la route se trouve à l'autre sommet relié à l'hypoténuse du triangle. Le troisième sommet du triangle est à côté de l'angle droit. Les côtés du triangle sont appelés a, b et c. Le côté a est le côté horizontal, le côté b est le côté vertical et le côté c est le côté diagonal.
Q3: Utilise le théorème de Pythagore pour trouver la longueur de X.
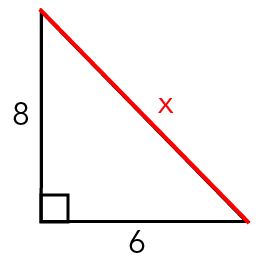
Image - Version texte
L'illustration montre un dessin d'un triangle rectangle. Il a un côté vertical annoté 8 et un côté horizontal annoté 6. Ces côtés sont colorés en noir. Le côté diagonal est coloré en rouge et porte l'inscription "x". Un petit carré est situé au sommet, en face du côté diagonal. Il indique que l'angle est de 90 degrés.
L'étape suivante consiste à se déplacer le long du réseau en utilisant le chemin le plus court. Cette étape utilise l'algorithme de Dijkstra (en anglais) pour trouver le plus court chemin le long d’un réseau. L'algorithme est très efficace car il n'examine pas tous les chemins possibles du début à la fin. Bien qu'il calcule le temps de chaque itinéraire possible au fur et à mesure qu'il s'éloigne du point de départ, il garde toujours la trace de l'itinéraire le plus court à un moment donné. Au fur et à mesure qu'il se déplace vers l'extérieur à la recherche de la fin, il donne la priorité à ce qui semble être le chemin le plus court et continue à se déplacer dans cette direction. Lorsqu'il atteint finalement la fin, il sait que le premier (et seul) chemin possible pour y parvenir est le plus court.
Pour ce faire, l'algorithme additionne chaque partie du chemin le plus court. Cela signifie qu'il calcule le temps nécessaire pour marcher sur le trottoir entre ton domicile et l'arrêt d’autobus. Il fait ensuite de même pour l'attente du bus, l'utilisation du bus et la correspondance avec un autre autobus. Enfin, il calcule le temps nécessaire pour le trajet d’autobus et pour marcher sur le trottoir jusqu'à ton école. Au fur et à mesure qu'il calcule le temps sur le réseau, il se déplace vers l'extérieur, comme indiqué sur l'image, jusqu'à ce qu'il trouve la destination.
L'analyse spatiale répète ce processus de nombreuses fois pour chaque point de la grille vers tous les autres points de la grille. Cela signifie que le nombre de calculs croît de manière exponentielle en fonction du nombre de points de la grille, au carré. Dans l'analyse pour la TTC, cela représente plus de 28 milliards de calculs (167 8822 = 28 184 365 924) !
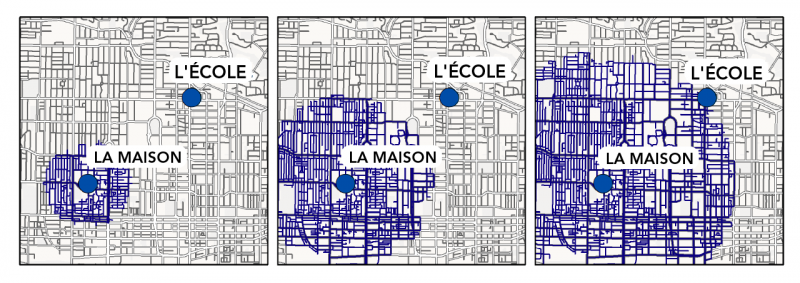
Image - Version texte
Ici, on voit trois cartes montrant tous les itinéraires possibles entre la maison et l'école. La carte de gauche montre des lignes bleues avec des itinéraires qui ne s'étendent que sur une courte distance depuis la maison. La carte du centre montre les itinéraires qui s'étendent de la maison jusqu'à environ la moitié de l'école dans plusieurs directions. La carte de droite montre tous les itinéraires qui relient le domicile à l'école.
La troisième étape utilise à nouveau le théorème de Pythagore pour passer du réseau à un point de la grille.
L’équipe de planification chez Jacob utilise le SIG pour réaliser ces trois étapes pour chaque point de la grille. Si le temps de trajet d'un point à un autre était inférieur à 45 minutes, le nombre d'emplois et de personnes à ce point final est compté. Ensuite, ces données sont analysées en utilisant les options de transport en commun actuelles et futures. Enfin, une carte fut créée montrant comment l'accès aux emplois changerait pour chaque endroit de Toronto avec l'ajout de nouveaux transports en commun.
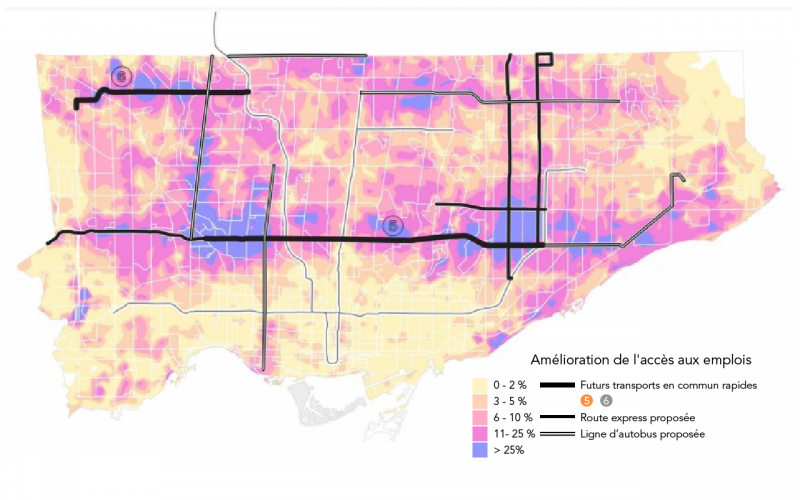
Image - Version texte
Cette carte de Toronto montre l'amélioration de l'accès aux emplois grâce à un itinéraire de transport en commun modifié. Les lignes grises représentent les itinéraires de transport en commun actuels. Les futurs itinéraires de transport en commun sont indiqués par des lignes noires. Les quartiers sont représentés par des couleurs différentes. Ces couleurs correspondent au pourcentage d'emplois supplémentaires auxquels les habitants de ce quartier pourraient accéder grâce aux projets de transport en commun proposés. Les zones dont le pourcentage de changement est le plus faible sont représentées en jaune et en orange. Les zones présentant un pourcentage de changement plus élevé sont indiquées en rose et en bleu. Les zones présentant le plus grand pourcentage de changement sont indiquées autour des futures lignes de transport rapide et des voies express.
Q4: Que remarques-tu à propos de l'emplacement des emplois par rapport aux nouvelles lignes de transport en commun ?
Cette carte montre comment les futurs projets de transport en commun pourraient améliorer l'accès aux emplois. Elle met également en évidence les quartiers qui bénéficieraient le plus de ces projets. Ces données ont ensuite été comparées aux indicateurs de bien-être des quartiers. Cela permet aux planificateurs d'identifier les quartiers qui ont le plus besoin d'améliorations en matière de transport en commun.

Image - Version texte
Photographie en couleur d'un tramway sur rails se déplaçant au centre d'une rue de Toronto. Le tramway est rouge et blanc avec des phares lumineux à l'avant. Il est long et de forme rectangulaire. Il est attaché à des câbles qui passent au-dessus de lui au milieu de la rue, à peu près à la hauteur d'un immeuble de deux étages. Des immeubles de deux et trois étages bordent la rue. La tour du CN est visible, s'étirant dans le ciel, à l'arrière-plan.
Parlons sciences apprécie le travail et les contributions de Tim Dickinson et Michael Grant de Jacobs dans l'élaboration de ce document d'information.
À propos de Jacobs
Chez Jacobs, nous mettons au défi l’aujourd'hui pour réinventer demain en résolvant les problèmes les plus critiques du monde pour des villes prospères, des environnements résilients, des résultats cruciaux à nos missions, des progrès opérationnels, des découvertes scientifiques et des procédés manufacturiers de pointe, en transformant des idées abstraites en réalités qui transforment le monde pour le meilleur. Avec un chiffre d'affaires d'environ 14 milliards de dollars et un effectif de plus de 55 000 personnes, Jacobs offre une gamme complète de services professionnels, notamment des services de conseil, des services techniques et scientifiques et des services de réalisation de projets pour le gouvernement et le secteur privé.
RÉPONSES
Q1: Ligne 2- Vert
Q2: Les réponses varient. Elles peuvent inclure des données telles que les temps de trajet, les possibilités d'emploi, les estimations démographiques, les itinéraires des projets de transport en commun actuels et futurs.
Q3: a2+ b2 = c2
62 + 82 = c2
100 = c2
√100= c
10 = c
Q4: Près des futurs projets de transport en commun
En savoir plus
Profil de carrière d’une gestionnaire de systèmes d’information géographique
Explore le profil de carrière de Stacey Corbett sur le site de Parlons sciences pour en savoir plus sur les carrières en analyse spatiale.
Profil de carrière d’un technicien en SIG
Explore le profil de carrière de Ralph Renso Ronquillo sur le site de Parlons sciences pour en savoir plus sur les carrières en analyse spatiale.
Bibliothèque Esri Story Maps - laissez-vous inspirer
Voici une galerie de cartes créées par ERSI Canada à l'aide de SIG pour raconter des histoires sur les lieux et la façon dont les gens vivent.
Références
Esri (2013). The Language of Spatial Analysis. Esri: Redlands.
Hertel, S., R. Keil and M. Collens (Feb 2016). Next Stop Equity: Routes to fairer transit access in the Greater Toronto and Hamilton Area. The City Institute at York University.
Jacobs (Dec 21, 2020) 360 Transit Alliance Joint Venture Selected to Lead Project Controls for Four Toronto Subway Lines.
King, D. and A.S. Shalaby (2016). Performance Metrics and Analysis of Transit Network Resilience in Toronto. Presented at the 95th Annual Meeting of the Transportation Research Board, Washington, D.C.
McCarty, B.A. (Jan 31, 2012). G-FAQ - What Is The Difference Between A Map And Spatial Analysis? Apollo Mapping.
