L’arithmétique de l’horloge

Nous avons tous appris à lire l’heure quand nous étions plus jeunes. Pour la plupart des gens, c’est assez simple. Mais derrière se cache une notion plus poussée qu’on appelle l’arithmétique modulaire. Cela pourrait s’expliquer comme suit. 

Et si tu voulais aller plus loin, disons chez tes grands-parents qui habitent une autre province?

Toutefois, sur une horloge, nous ne comptons pas de façon ordinaire. Pour beaucoup de gens, après 12 h (midi), la prochaine unité est 1 h, et non 13 h, et la suivante est 2 h, et non 14 h. Mais il ne s’agit là que de conventions. Beaucoup disent aussi 14 h au lieu de 2 h! Mais, dans un cas comme dans l’autre, on parle bel et bien de 2 h après 12 h. 

Ainsi, sur une horloge, 14 veut dire la même chose que 2.

Cela veut-il dire que 14 = 2? Dans un certain sens, peut-être que oui…

Nombres congrus modulo

Dans notre exemple, les nombres 14 et 2 peuvent être considérés comme des « égaux de l’horloge ». Les mathématiciens et mathématiciennes ont une façon particulière d’exprimer cette réalité. Ils disent que ces nombres sont des congrus modulo 12 si leur différence est de 12, 24, 36 ou n’importe quel autre multiple de 12. Les nombres 2 et 14 en sont un exemple. Sur une horloge, ils signifient la même chose. Mathématiquement, cela s’exprime de la manière suivante :

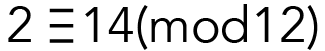
La relation de congruence modulo n est notée par le symbole « ≡ ». Dans l’expression ci-dessus, 12 est le modulus. Voici un autre exemple de deux nombres congrus modulo 12 :

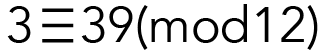
Ils le sont parce que la différence entre 39 et 3 est 36, ce qui se divise par 12 (sans reste). Bien sûr, tous les nombres ne sont pas congrus modulo 12. Par exemple :

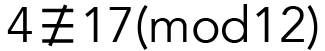
La différence entre 4 et 17 est 13, et ce nombre n’est pas divisible par 12.

Maintenant, imaginons un monde où les horloges ont 7 heures au lieu de 12. Cela peut sembler étrange, mais nous pourrons ainsi compter en utilisant le modulus 7. Ici, nous pourrons dire que deux nombres sont congrus modulo 7 si leur différence est divisible par 7, par exemple :

Les nombres 2 et 9 sont congrus modulo 7, parce que leur différence (9 – 2 = 7) est divisible par 7. Toutefois :

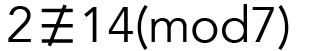
parce que leur différence (14 – 2 = 12) n’est pas divisible par 7.

L’arithmétique modulaire

Revenons à notre horloge normale de 12 heures. Dans un système modulo 12, la réponse à n’importe quelle addition doit être inférieure à 12. Le premier problème que nous avons rencontré dans cette section (celui de la visite chez les grands-parents) avait pour somme « 9 + 5 ». En arithmétique régulière, on dirait que « 9 + 5 = 14 », mais en arithmétique modulo 12, 14 est un nombre trop grand (il n’apparaît pas sur l’horloge). Il faut donc trouver son équivalent. 

Comme nous savons que 14 est congru à 2 modulo 12 :

9 + 5 ≡ 2(mod12)

L’expression 2 (mod 12) est donc la bonne réponse à la question 9 + 5.

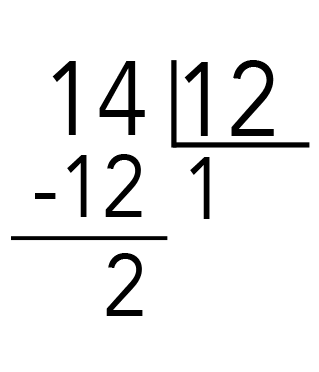
Si la somme des deux nombres est un multiple entier du modulus, on peut écrire un zéro ou le chiffre lui-même devant ce dernier:

 3 + 4 ≡ 0(mod7)

OU 

 3 + 4 ≡ 7(mod7)

Les mathématiciens et mathématiciennes préfèrent utiliser le 0, mais le 7 est aussi acceptable dans le cas ci-dessus.

Tente de résoudre les problèmes suivants en arithmétique modulo 7. Souviens-toi que ta réponse doit se situer entre 0 et 6.

Les nombres 12 et 7 ne sont pas les seuls modulus qu’on puisse utiliser. On peut choisir n’importe quel chiffre. Nous pourrions très bien faire des mathématiques avec des modulos 5 999, 327 ou 16, si nous le voulons! 

L'arithmétique modulaire dans la vie courante

L'arithmétique modulaire a de nombreuses applications en cryptographie et en informatique. Elle est souvent utilisée pour détecter des erreurs dans les numéros d'identification. Pense aux types de numéros d'identification que nous utilisons tous les jours. Les cartes de crédit, les comptes bancaires et les codes-barres des produits sont tous composés de longues chaînes de chiffres. Ces numéros doivent être correctement échangés par les systèmes informatiques. Pense à lorsque tu utilises une carte de crédit pour acheter quelque chose en ligne. Imagine si deux des chiffres étaient inversés ou mal tapés. L'arithmétique modulaire est utilisée pour détecter ce genre d'erreurs. C’est une première étape de vérification avant celle de la banque. 

Pour aider à détecter les erreurs, de nombreux nombres importants comportent aussi un nombre de contrôle. C'est généralement le dernier chiffre d'un nombre. Il est utilisé dans le cadre d'un algorithme d'arithmétique modulaire pour vérifier que le nombre ne contient pas d'erreurs. L'algorithme mod 10 ou algorithme de Luhn est un algorithme couramment utilisé. Cet algorithme consiste à doubler puis à additionner tous les chiffres dans un ordre particulier. Le nombre est correct si le total modulo 10 est égal à 0, ce qui signifie qu'il s'agit d'un multiple de 10. Cet algorithme est utilisé pour valider les numéros d'assurance sociale canadiens, les numéros de cartes de crédit et bien d'autres. Bien que nous ne le réalisons pas, nous utilisons ce genre d'application d'arithmétique modulaire tous les jours.

SOLUTIONS

Questions 1

Est-ce que 3 ≡ 9(mod7)?

3 ≡ 9(mod7)

Non, parce que la différence entre ces nombres (9 – 3 = 6) n’est pas divisible par 7.

Questions 2

Est-ce que 1 ≡ 7(mod7)?

1 ≢ 7(mod7)

Non, parceque la différence entre ces nombres (7 – 1 = 6) n’est pas divisible par 7.

Questions 3

Est-ce que 2 ≡ 16(mod7)?

2 ≡ 16(mod7)

Oui, parce que la différence entre ces nombres (16 – 2 = 14) est divisible par 7.

Questions 4

3 + 18 = 0(mod7)

3 + 18 = 21 

21 ÷ 7 = 3 Comme il n’y a pas de reste, on met un 0 devant le modulus (mod7).

Questions 5

2 + 4 = 6(mod7)

2 + 4 = 6 

Le nombre 6 ne se divise pas en 7 sans reste. En fait, il ne se divise pas du tout en 7; il devient donc lui-même le reste (6), et se place ainsi devant le modulus(mod7).

Questions 6

19 + 10 = 1(mod7)

19 + 10 = 29

29 ÷ 7 = 4. Le reste est 1; c’est donc ce qu’on place devant le modulus(mod7).