Diagrammes de Venn et d’Euler

Diagrammes de Venn et d’Euler (Parlons sciences)
Apprends deux façons de représenter les ensembles - les diagrammes de Venn et d'Euler.
Diagrammes de Venn
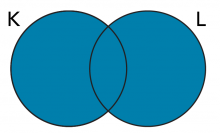
On utilise parfois des schémas pour représenter des ensembles. On peut notamment penser aux diagrammes de Venn, qui nous aident à visualiser les relations entre divers ensembles. Généralement, les diagrammes de Venn apparaissent comme deux cercles joints en partie, mais ils peuvent en compter davantage. Dans certains cas, les diagrammes n’illustrent pas les éléments les composant, comme on le voit dans l’exemple des ensembles K et L ci-dessous.
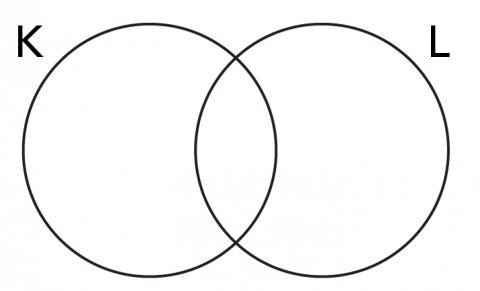
Chacun des cercles représente alors tous les éléments d’un ensemble. Même s’ils sont vides, on peut donc se poser le même genre de questions au sujet d’éventuels sous-ensembles, intersections et unions.
Est-ce que K ⊆ L (est-ce que K est à l’intérieur de L)? NON.
Est-ce que L ⊆ K (est-ce que L est à l’intérieur de K)? NON.
Question 1: Qu’est-ce que K ∩ L? (Quelle est l’aire comprise dans les deux ensembles?) Dessine le schémas et noircis l’aire représentant ta réponse ci-dessous.
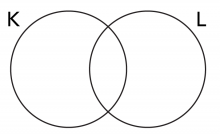
Question 2: Qu’est-ce que K ∩ L? (Quelle est l’aire totale représentant ce qui est dans l’ensemble K, l’ensemble L ou les deux?). Dessine le schéma et noircis l’aire représentant ta réponse ci-dessous.

Essaie avec ces ensembles :
E = {1, 3, 8, 9, 14, 17}
F = {0, 14, 3, 5, 10, 20}
Questions 3 : Utilise un diagramme de Venn pour illustrer les ensembles E et F.
Qu’est-ce que E ∩ F?
Qu’est-ce que E ∪ F?
Qui était Venn?
John Venn (1834-1923) était un logicien anglais (il étudiait la pensée logique) et un philosophe dont on se souvient pour avoir inventé le diagramme qui porte son nom – le diagramme de Venn.
Venn a été élevé par son père qui était pasteur à l’Église d’Angleterre (sa mère est morte alors qu’il était très jeune). Il est allé à l’université de Cambridge où il a obtenu une bourse de mathématique lors de sa 2e année. Bien qu’il excellait en mathématique à l’école, il est devenu pasteur comme son père et son grand-père après avoir gradué.
Venn n’a jamais cessé de penser aux mathématiques et donc, après avoir fait du travail religieux pour quelques années, il est retourné à Cambridge en 1862 où il a enseigné la logique et les probabilités. Il s’est marié en 1867 et a eu un fils, John. Son fils John est éventuellement devenu le président du collège Queen à l’Université de Cambridge, où il a fait des projets de recherche importants avec son père.
Le diagramme de Venn a été publié pour la première fois en 1880 dans un article intitulé "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings." (pouvant être traduit comme : Les représentations mécaniques et sous forme de diagramme des propositions et raisonnements) dans la revue "Philosophical Magazine and Journal of Science."
Diagrammes d’Euler
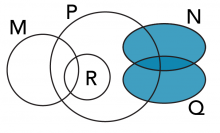
On peut aussi montrer les relations entre divers ensembles à l’aide de diagrammes d’Euler. Ils ressemblent aux diagrammes de Venn, mais tendent à être plus complexes, en illustrant souvent des sous-ensembles en plus des intersections et des unions. Dans un diagramme d’Euler, la taille et la forme des cercles ou des ovales n’ont pas d’importance; il ne faut considérer que leur manière de se chevaucher ou non.
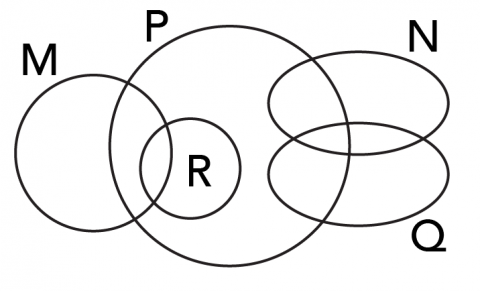
Question 4:
Y a-t-il des sous-ensembles (⊆) d’un autre ensemble ?
Si oui, lesquels ?
Question 5:
A) Noircis N ∪ Q

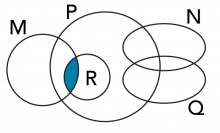
B) Noircis M ∩ R

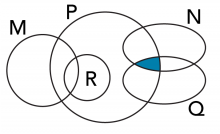
C) Noircis P ∩ N ∩ Q

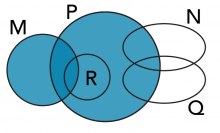
D) Noircis M ∪ P ∪ R

Existe-t-il une intersection N ∩ R? Non. Les ensembles N et R ne se chevauchent pas. Selon la théorie des ensembles, il s’agit d’un ensemble nul, ou d’un ensemble vide, parce qu’il ne contient rien. Le symbole d’un ensemble vide est « ∅». Voici un autre exemple d’ensemble vide :
L’ensemble G contient toutes les girafes qui se trouvent dans la classe de Mme Tremblay. G = { } = ∅
Applications pratiques des diagrammes de Venn et d’Euler
Les diagrammes de Venn et d'Euler sont utiles dans une variété de contextes différents. Les deux types de diagrammes nous aident à visualiser les concepts et les relations. Cela peut nous aider à comprendre plus facilement des informations complexes. Ces diagrammes utilisent la même structure pour représenter une grande variété de contenu.
Par exemple, les diagrammes de Venn sont souvent utilisés pour résoudre des problèmes mathématiques. Représenter une question sous forme de diagramme de Venn peut souvent la rendre plus facile à comprendre et à résoudre. Les entreprises utilisent souvent les diagrammes de Venn pour comparer des produits, analyser les concurrents et prendre des décisions. Les diagrammes de Venn représentent beaucoup d'autres types d'informations pratiques, de la chimie à la géographie. Ils peuvent même être utilisés pour l'humour ou pour représenter des questions philosophiques difficiles. Les diagrammes de Venn et d'Euler sont un moyen simple de représenter toutes sortes d'informations.
SOLUTIONS
Question 1:
Quelle est l’aire de K ∩ L? (Quelle est l’aire comprise dans les deux ensembles?) Noircis ta réponse ci-dessous.
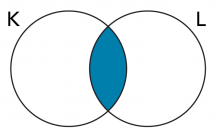
Question 2:
Quel est K ∪ L? (Quelle est l’aire totale des deux ensembles et de leur intersection?) Noircis ta réponse ci-dessous.
Question 3:
Utilise un diagramme de Venn pour illustrer les ensembles E et F.
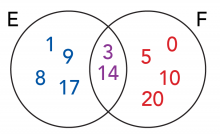
E ∩ F = {3, 14}
E ∪ F = {0, 1, 3, 5, 8, 9, 10, 14, 17, 20}
Question 4:
Y a-t-il des sous-ensembles (⊆) des ensembles ci-dessus? Si oui, lequel ou lesquels?
Oui, R est un sous-ensemble de P (R ⊆ P).
Question 5:
A) Noircis N ∪ Q
B) Noircis M ∩ R
C) Noircis P ∩ N ∩ Q
D) Noircis M ∪ P ∪ R
En savoir plus
Cette page de Mathématiques faciles offre des exercices interactifs sur les diagrammes de Venn.
Le diagramme de Venn (intersection, union et ensemble complémentaire)
Cette page de Allo Prof présente la théorie et des exercices sur les diagrammes de Venn.
Références
Indeed. (2020, February 4). What is a Venn Diagram and What Is It Used For?.
KidSmart. (2019, September 13). What is a Venn Diagram and When to Use It?.
